100.相同的树
难度:容易
给你两棵二叉树的根节点 p 和 q ,编写一个函数来检验这两棵树是否相同。
如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
示例 1:
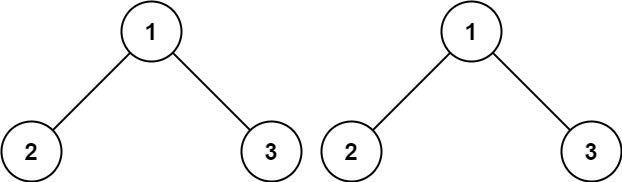
输入:p = [1,2,3], q = [1,2,3]
输出:true示例 2:
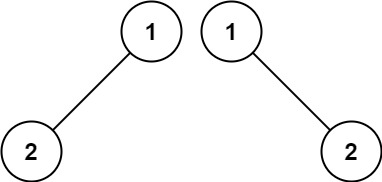
输入:p = [1,2], q = [1,null,2]
输出:false示例 3:
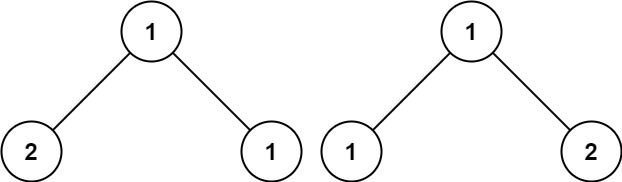
输入:p = [1,2,1], q = [1,1,2]
输出:false提示:
- 两棵树上的节点数目都在范围
[0, 100]内 -10^4 <= Node.val <= 10^4
递归法
这道题和 101 题几乎是一样的。
我们要比较的是两个树,所以在递归遍历的过程中,也是要同时遍历两棵树。
递归三部曲:
确定递归函数的参数和返回值
因为我们要比较的是两个树,参数自然也是 p 树节点和 q 树节点,返回值是 bool 类型。
javaboolean isSameTree(TreeNode p, TreeNode q);确定终止条件
要比较两个节点数值相不相同,首先要把两个节点为空的情况弄清楚!否则后面比较数值的时候就会操作空指针了。
- p、q 节点都为空,则对称,返回
true - p、q 节点有一个为空,则不对称,返回
false
此时已经排除掉了节点为空的情况,那么剩下的就是p、q节点不为空的情况:
- p、q 节点都不为空,比较节点数值,不相同就返回
false
此时 p、q 节点不为空,且数值也不相同的情况我们也处理了。
javaif (p == null && q == null) { return true; } else if (p == null || q == null) { return false; } else if (p.val != q.val) { return false; }- p、q 节点都为空,则对称,返回
确定单层递归的逻辑
此时才进入单层递归的逻辑,单层递归的逻辑就是处理 左右节点都不为空,且数值相同 的情况。
- 比较 p、q 对应左右孩子是否相同,相同就返回
true,有一个不相同就返回false。
javareturn isSameTree(p.left, q.left) && isSameTree(p.right, q.right);- 比较 p、q 对应左右孩子是否相同,相同就返回
代码展示
java
public boolean isSameTree(TreeNode p, TreeNode q) {
if (p == null && q == null) {
return true;
} else if (p == null || q == null) {
return false;
} else if (p.val != q.val) {
return false;
}
return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
}时间复杂度:O(n),其中 n 是二叉树的节点数。每一个节点恰好被遍历一次。
空间复杂度:O(1),因为这种做法没有使用队列,所以大大降低了空间复杂度。
队列迭代法
首先我们引入队列,这是把递归程序改写成迭代程序的常用方法。
使用一个队列,并成对地将两棵树的节点加入队列,然后逐一比较这些节点。
算法的核心逻辑:
- 如果根节点都为空,树自然是相同的,返回
true。 - 初始化队列,使用一个队列
queue来存储待比较的节点对。初始时,将两棵树的根节点成对加入队列。 - 进入一个循环,每次循环中,从队列中取出两个节点(分别来自两棵树的相同位置)进行比较:
- 如果两个节点都为空,继续下一轮比较。
- 如果一个节点为空而另一个不为空,树不相同,返回
false。 - 如果两个节点都不为空但值不同,树不相同,返回
false。 - 如果两个节点都不为空且值相同,则将它们的左子节点和右子节点分别成对加入队列,以待后续比较。
- 如果队列为空,则所有对应的节点都匹配成功,树是相同的,返回
true。
代码展示
java
public boolean isSameTree(TreeNode p, TreeNode q) {
// 如果根节点为空,则树自然是相同的
if (p == null && q == null) {
return true;
}
// 使用一个队列存储节点,成对地将节点加入队列
Deque<TreeNode> queue = new LinkedList<>();
// 成对地将根节点加入队列
queue.add(p);
queue.add(q);
while (!queue.isEmpty()) {
// 每次取出两个节点进行比较
TreeNode curP = queue.poll();
TreeNode curQ = queue.poll();
// 如果两个节点都为空,继续下一轮循环
if (curP == null && curQ == null) {
continue;
}
// 如果一个节点为空而另一个不为空,或者两个节点的值不相等,说明两树不相等,返回false
else if (curP == null || curQ == null || curP.val != curQ.val) {
return false;
}
// 成对地将子节点加入队列,保持位置的一致
queue.add(curP.left);
queue.add(curQ.left);
queue.add(curP.right);
queue.add(curQ.right);
}
// 如果所有节点都相等,返回true
return true;
}时间复杂度:O(n),其中 n 是二叉树的节点数。每一个节点恰好被遍历一次。
空间复杂度:O(n),最差情况下,即当树为满二叉树时,最多有 (n+1)/2 个树节点 同时 在 queue 中,故使用 O(n) 大小的额外空间。
总结
针对二叉树的问题,解题之前一定要想清楚究竟是前中后序遍历,还是层序遍历。
