459.重复的子字符串
难度:容易
给定一个非空的字符串 s ,检查是否可以通过由它的一个子串重复多次构成。
示例 1:
输入: s = "abab"
输出: true
解释: 可由子串 "ab" 重复两次构成。示例 2:
输入: s = "aba"
输出: false示例 3:
输入: s = "abcabcabcabc"
输出: true
解释: 可由子串 "abc" 重复四次构成。 (或子串 "abcabc" 重复两次构成。)提示:
1 <= s.length <= 10^4s由小写英文字母组成
解题思路(暴力枚举)
- 通过外层循环遍历所有可能的子串长度,但只考虑那些能被整个字符串长度整除的子串长度。
- 对于每一个这样的子串长度,函数检查整个字符串是否可以被这个子串完整地、重复地覆盖。
- 这种检查是通过内层循环实现的,该循环遍历字符串的每个字符,并将其与假定的重复子串中的对应字符进行比较。
- 如果在任何时候字符不匹配,内层循环会提前终止,并且外层循环继续尝试下一个子串长度。
- 如果找到了完全匹配的子串,则函数返回
true,否则,遍历完所有可能的子串长度后返回false。
代码展示
public boolean repeatedSubstringPattern(String s) {
// 获取字符串的长度
int ls = s.length();
// 外层循环:尝试每一个可能的子串长度
for (int i = 1; i <= ls / 2; i++) {
// 如果i是字符串长度的因子,则进行检查
if (ls % i == 0) {
int j = i;
// 内层循环:遍历字符串,从第i个字符开始
// 将每个字符与它应该匹配的字符(即它在重复子串中的对应字符)进行比较
while (j < ls) {
// 一旦发现不匹配,立即跳出循环
if (s.charAt(j) != s.charAt(j % i)) {
break;
}
j++;
}
// 如果整个字符串匹配了重复的子串模式,则返回true
if (j == ls) {
return true;
}
}
}
// 如果没有找到任何重复的子串模式,则返回false
return false;
}时间复杂度: O(n^2)
空间复杂度: O(1)
双倍字符串法
算法原理:把字符串翻倍,掐头去尾,如果原字符串在其中,那么原字符串就是周期串 。
证明匹配意味着周期性
假设我们有字符串 s ,把它的头尾字符分别染上黄色和蓝色:

把字符串 s 接到自身后面,然后掐头去尾,形成新字符串 s':
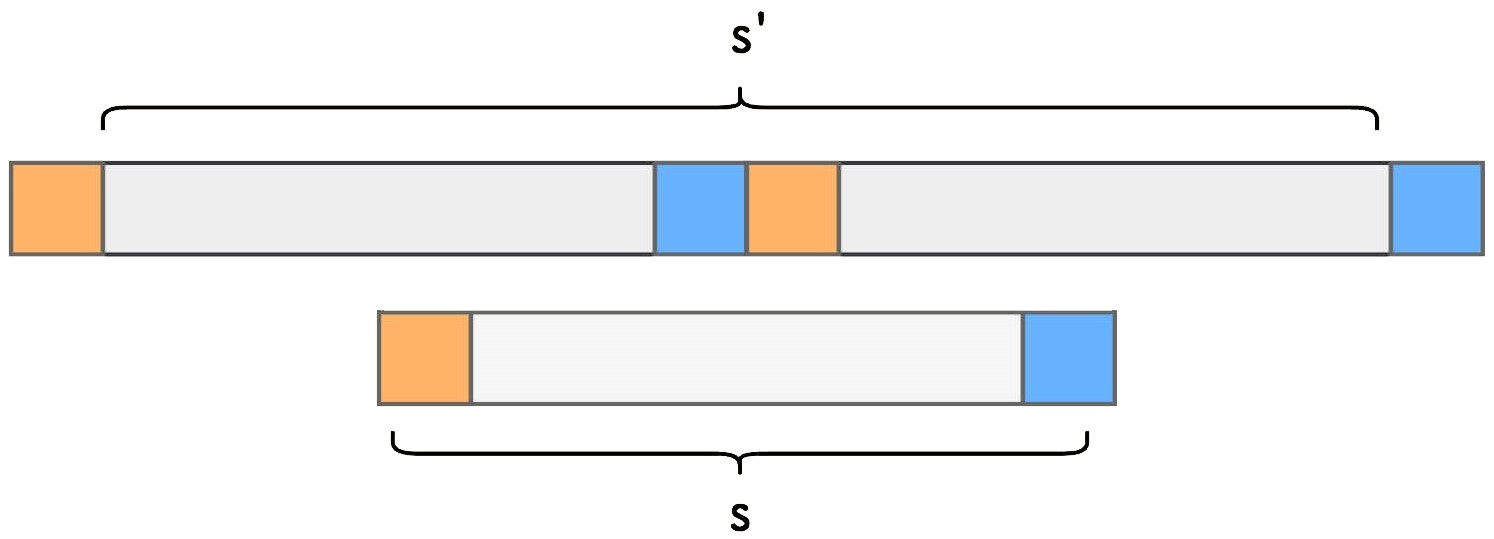
如果原字符串 s 在新字符串 s' 中真的存在,能说明 s 是一个周期串吗?答案是能。
不妨设右边匹配的少一些。对其中的任一字符 A ,可以按照如下的规则推演:
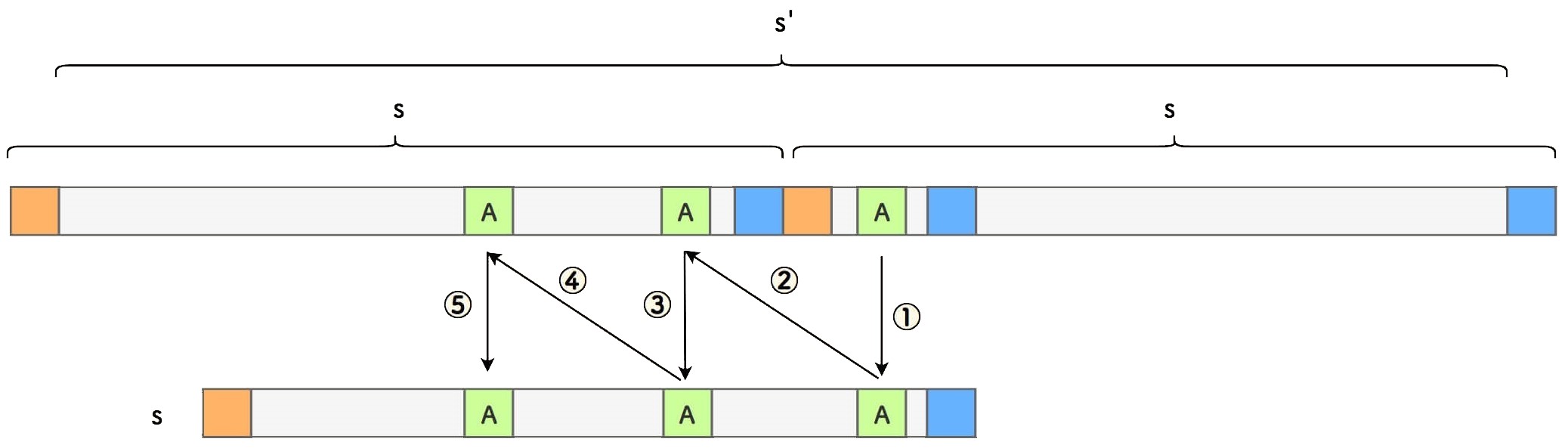
推演说明:
- 由于上下字符串匹配,所以有 ① 号推演。
- 由于和左上方的自身相等,所以有 ② 号推演。
- 如此反复。
如此,任一此区间上的字符 A 会在 s 中周期性出现,即说明字符串 s 是周期串。
证明周期性意味着匹配
**反过来,如果一个字符串 s 是周期串,那么它一定在对应的 s' 中吗?**答案也是肯定的,证明过程:
任何一个周期串可以表达为: 由某个模式子串的重复多次构成。
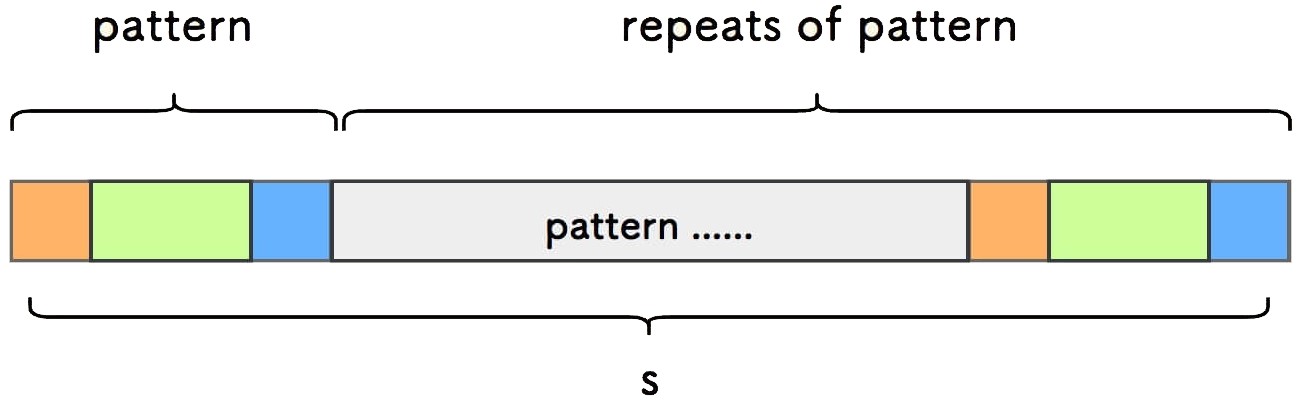
将周期串 s 的头字符对齐在第一个模式串后面, 每次右移一个模式串的长度。
可知,s 会在 s' 中有匹配,且可以有多个匹配。
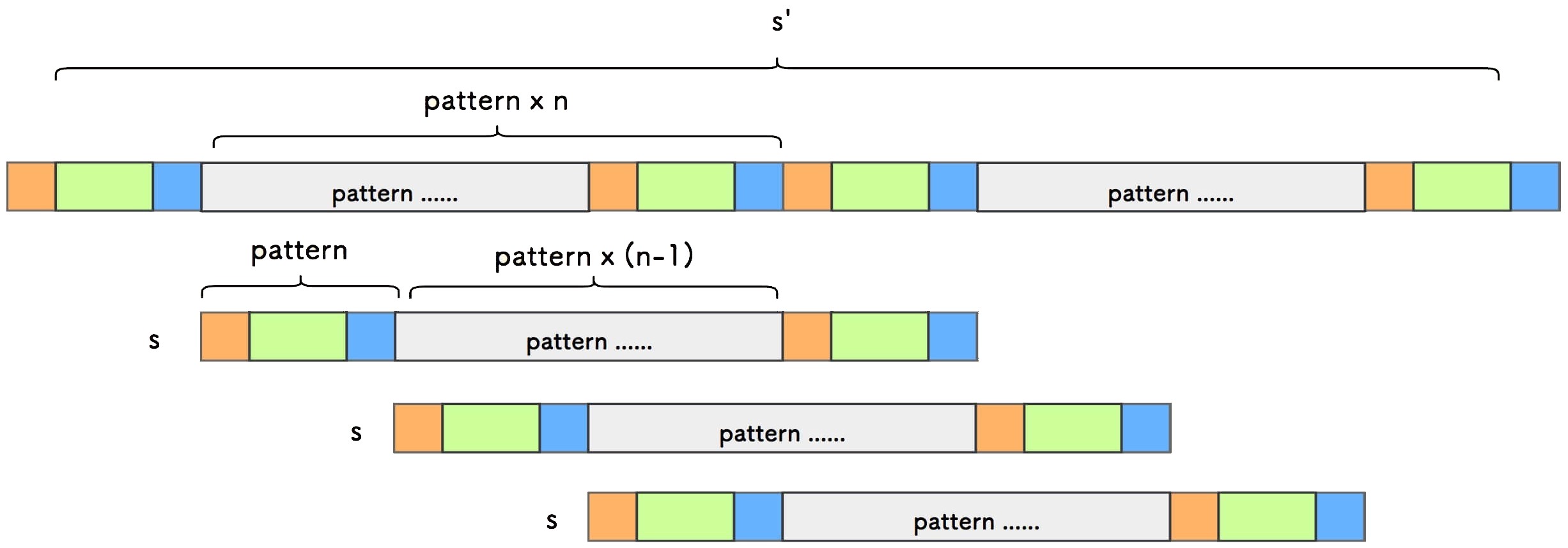
图中可看出, 因为模式串重复 n 次,所以会有 n 次匹配 。
构造双倍串 s' 时,移除头尾字符, 正是 为了剔除最左和最右的两次必然匹配,确保只有中间的 n 次匹配才用到了周期串重复模式串的性质。
结论
综上两方面说明了充分性和必要性,结论:如果字符串在其掐头去尾的双倍字符串中,它就是周期串。
代码展示
public boolean repeatedSubstringPattern(String s) {
String str = s + s;
str = str.substring(1, str.length() - 1);
return str.contains(s);
}本方法的实现,依赖语言自建的字符串搜索方法,故不做复杂度分析。
KMP 法
假设要判断的字符串为 s ,将其尾部字符标记为蓝色,取字符串 q 为不包含 s 尾部字符的部分,取 c 为 q 的 最长相等前后缀。
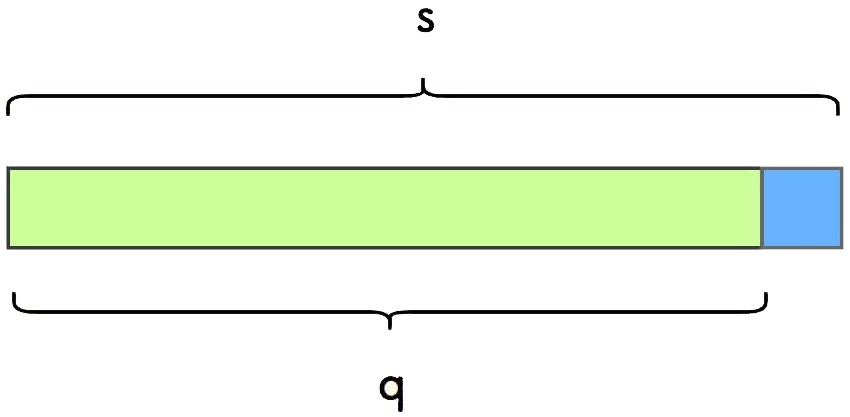
相等前后缀的意思是,它是既出现在字符串最前面、也出现在字符串最后面的真子串,比如如果 s 是字符串串 "abcabcabc" ,则 q 是 "abcabcab" ,q 的最长相等前后缀 c 是 "abcab" :
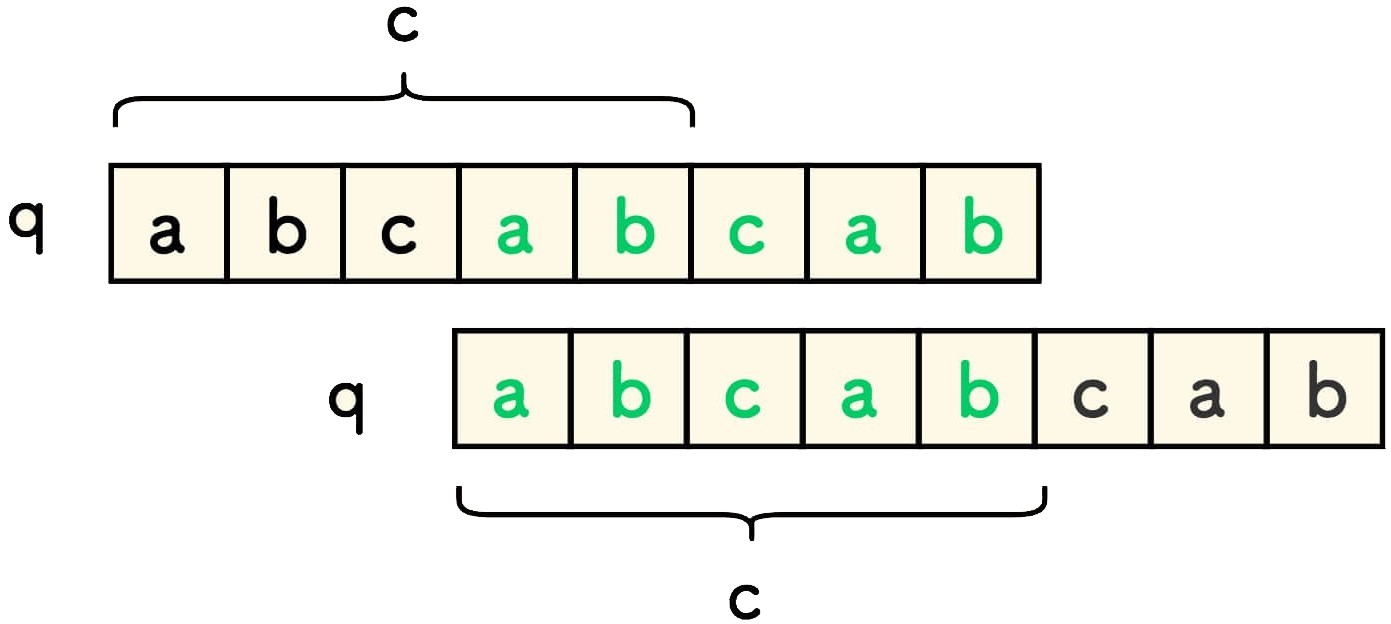
使用 kmp 法求解此题的原理是:s 是周期串等价于 len(s) 是 len(q) - len(c) 的倍数
证明 s 是周期串意味着 len(s) 是 len(q) - len(c) 的倍数
假设字符串 s 是一个周期串,它由模式串 p 重复多次构成:
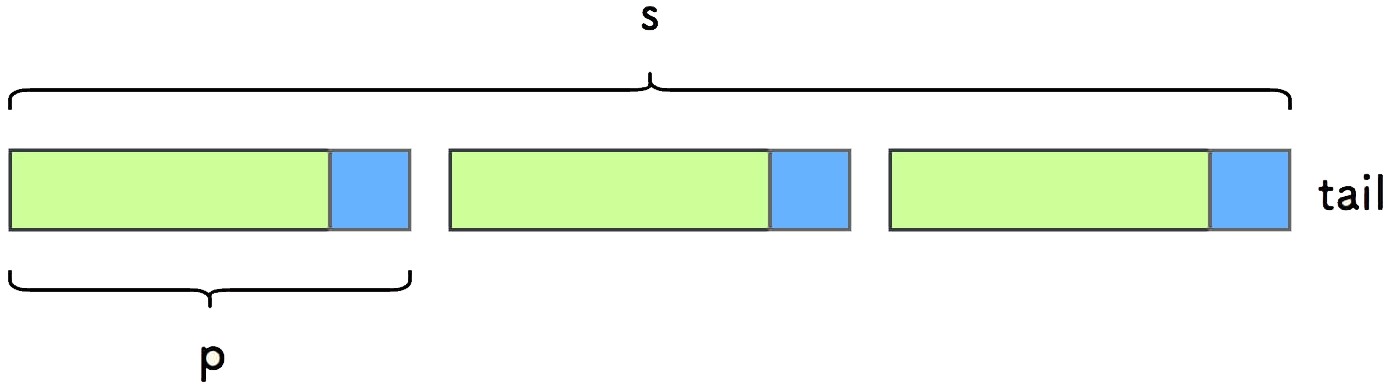
取字符串 q 为不包含 s 尾部字符的部分, 取 c_1 为 q 中剔去开头第一个模式串 p 后的部分:
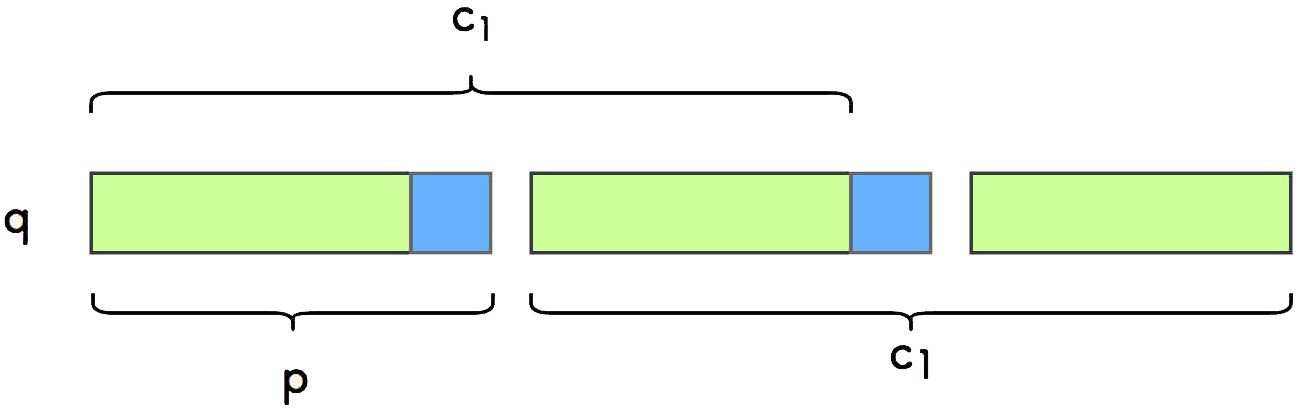
显然,字符串 c_1 是 q 的一个 相等前后缀,比如周期串 "abcabcabc" ,对应的 c_1 则是 "abcab" :
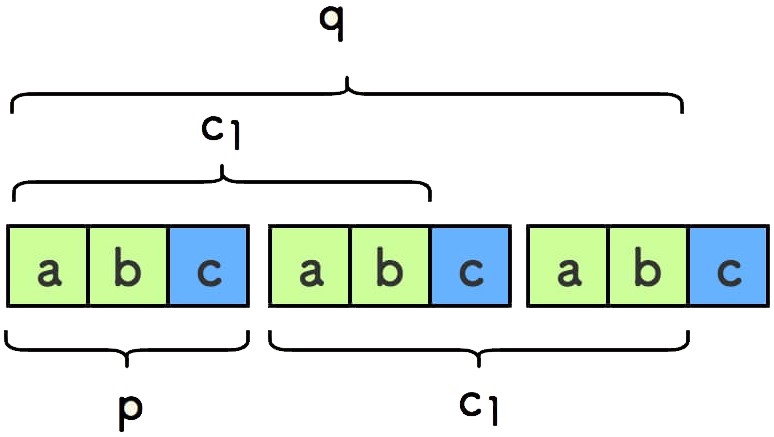
实际上,c_1 就是 q 最长的前后公共缀 c,由此可知周期长度是 len(p) = len(q)-len(c) 。
证明了:若字符串 s 是周期串,所以其长度一定是周期长度的倍数。
c_1 就是 q 最长的前后公共缀 c 的证明
我们采用反证法,假设存在一个字符串 c' 也是 q 的前后公共缀,而且它比 c_1 长一位,另外,假设尾部字符为 A 。
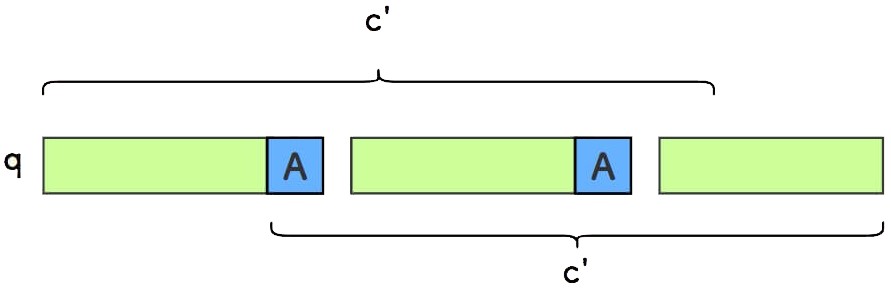
现在有两条性质:
- 周期性质:字符串
s的周期性。 - 相等前后缀性质:
c'是q的相等前后缀。
我们反复利用这两条性质:
由于「相等前后缀性质」,
q的第一个字符也是A。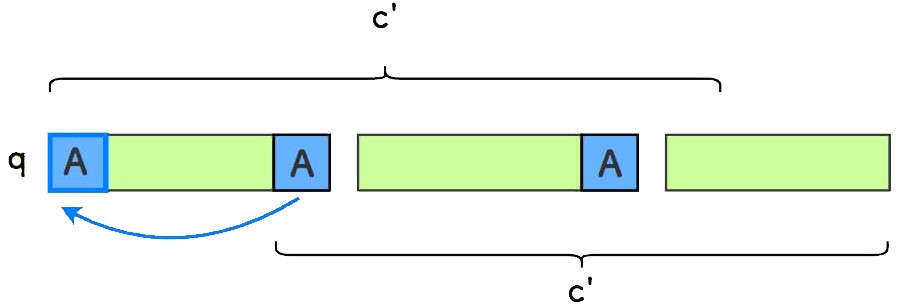
由于「周期性质」,后续的循环子串中的第一个字符也是
A。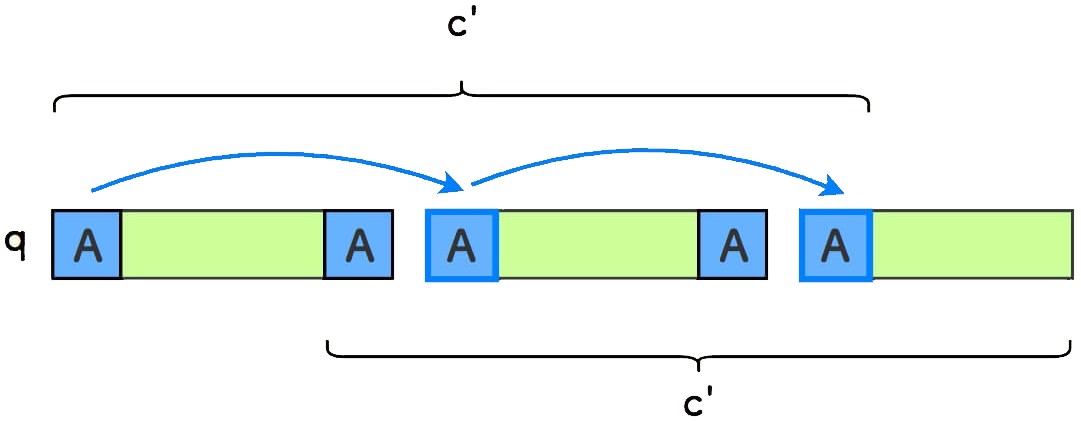
由于「前后公共缀性质」,
q的第二个字符也是A。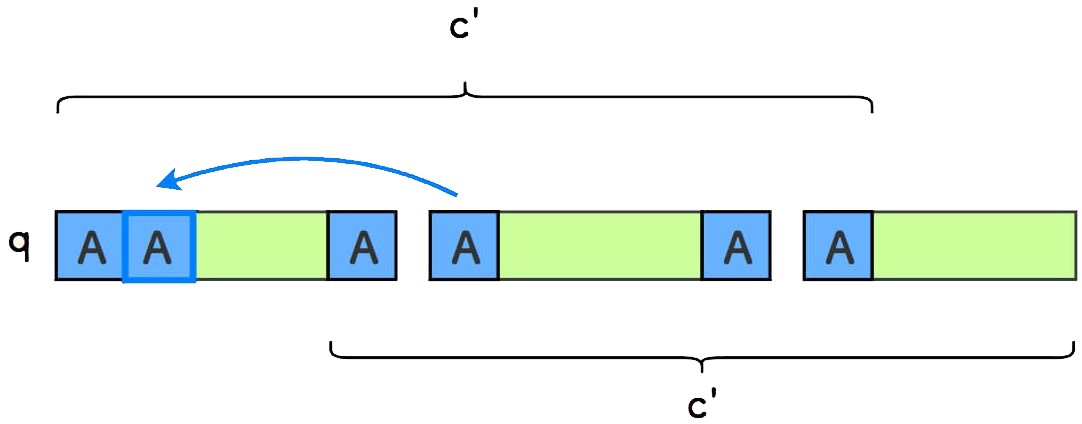
由于「周期性质」,后续的循环子串中的第二个字符也是
A。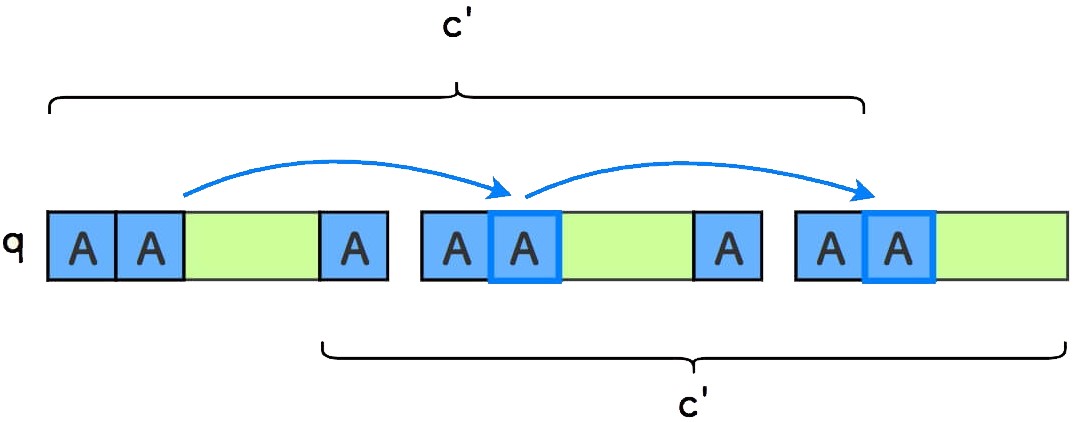
如上反复进行,最终,推断整个
q以及s都由字符A构成。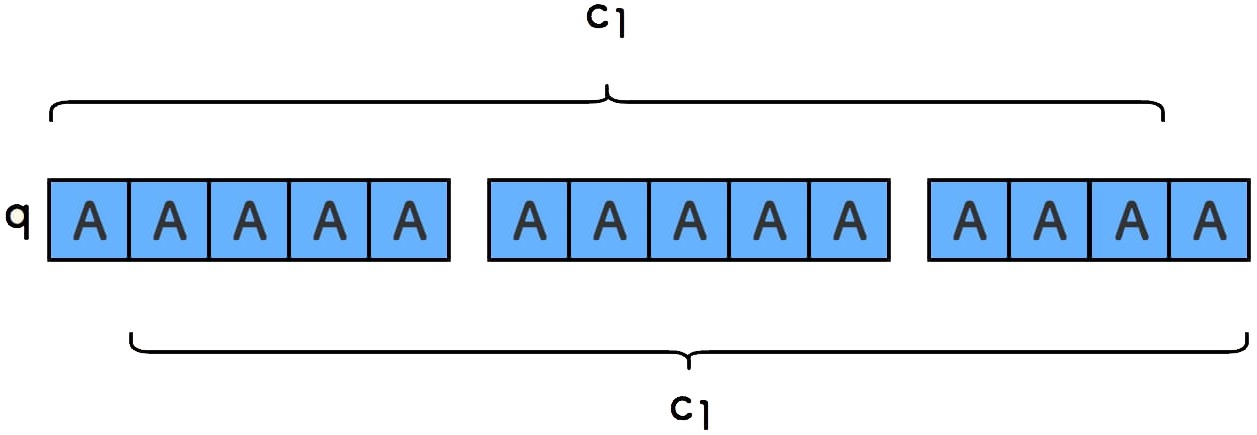
此时的模式串 p 即单个字符 A ,c_1 如上图,长度是 len(q)-1 。
相等前后缀是真子串,显然,不会存在比它更长的前后公共缀,造成矛盾。因此,所定义的 c_1 就是 q 的最长前后公共缀 c 。
证明 len(s) 是 len(q) - len(c) 的倍数意味着 s 是周期串
令 d = len(q)-len(c) , 如果字符串 s 的长度是 d 的倍数,是否 s 一定是周期串?
此时字符串 s 一定可以按照每 d 个字符一份,切分为整数个小串:
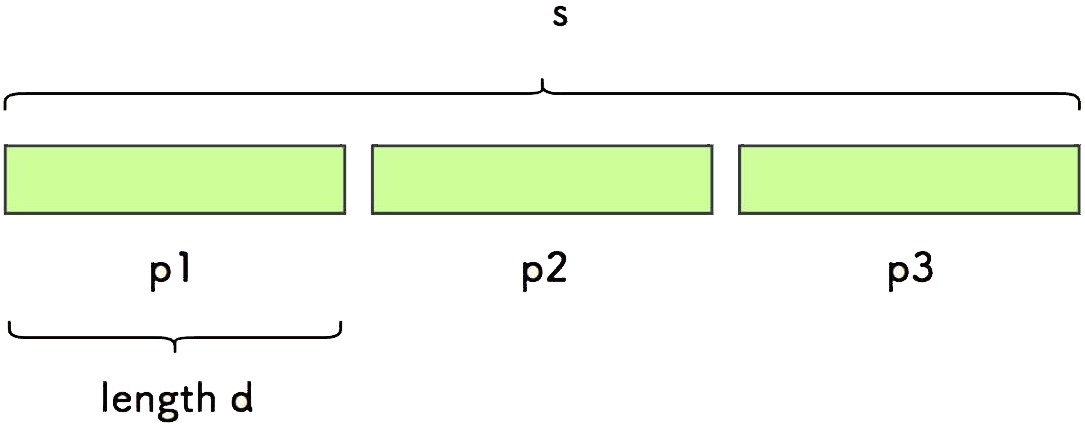
同样假设尾巴字符是蓝色的 A , 剔除尾巴字符后 q 和 其最长前后公共缀 c 如下所示:
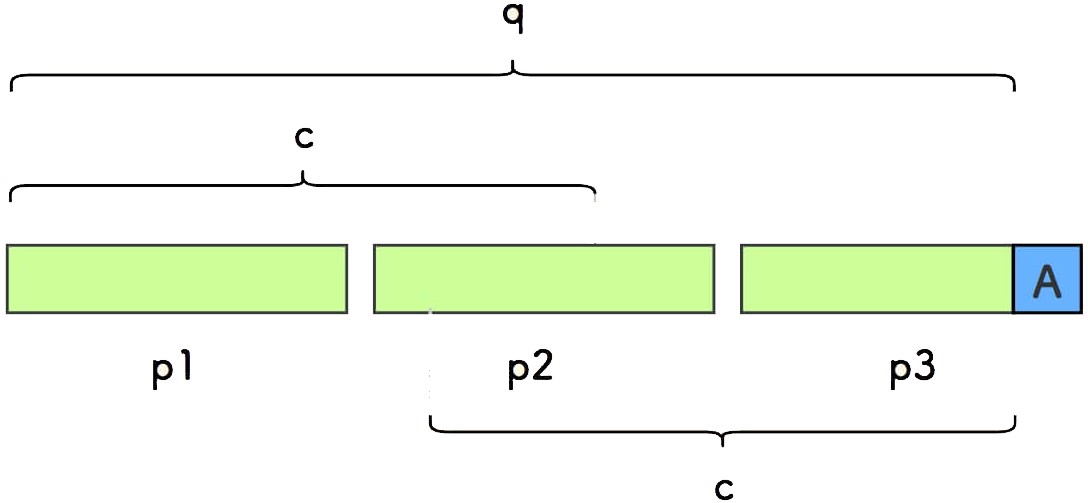
根据 d = len(q) - len(c) , 我们知道 len(c) + 1 = len(q) - d + 1 。
又因 len(q) = len(s) - 1 ,且 len(s) 可以写作 len(s) = k * d 。
所以 len(c) + 1 = k * d - d = (k - 1) * d ,说明 len(c) + 1 是 d 的倍数。
因此,在下图中, c 必然上下对齐于某个小串的开头。
又因 len(c) + 1 = (k - 1) * d ,所以 c 就是 q 中剔除第一个小份串 p1 的部分。
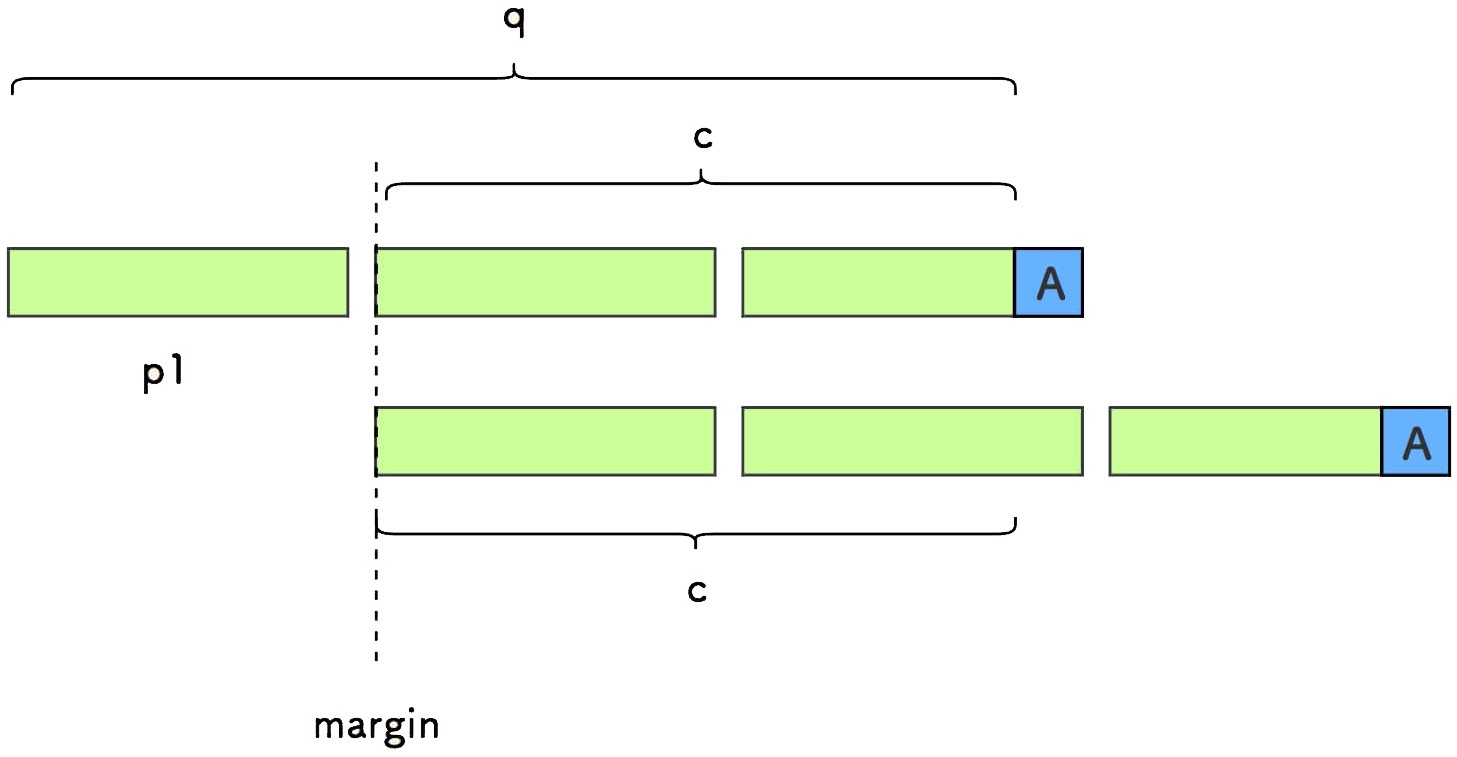
下面将说明,s 是一个周期串。
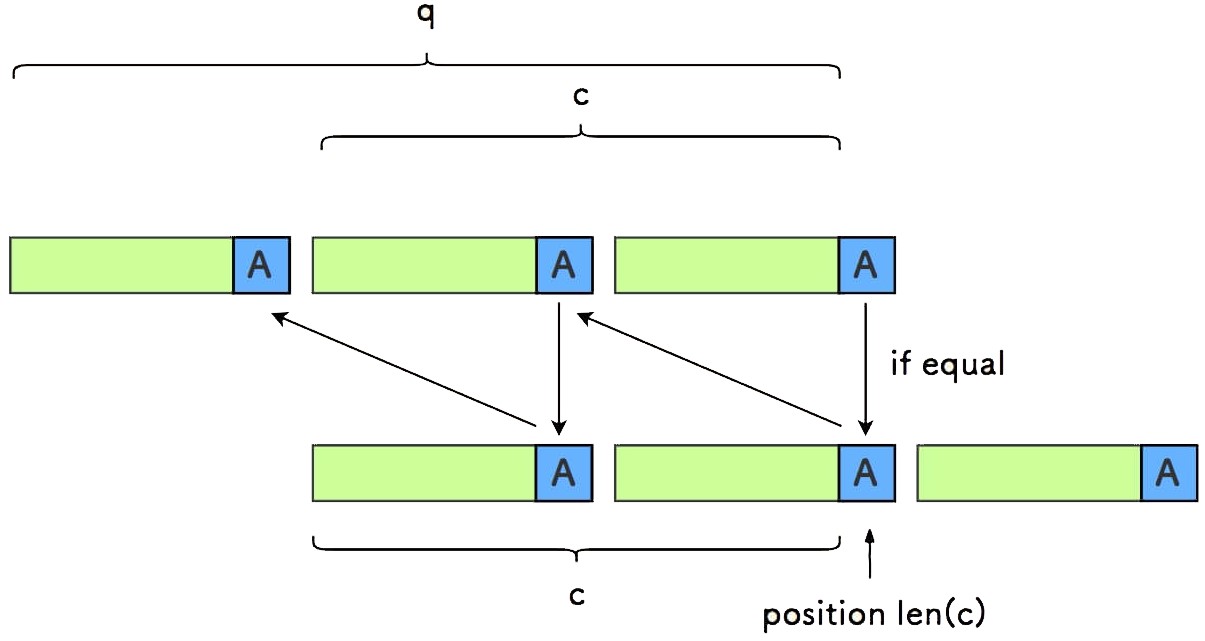
在最后一个小份串,从尾部取倒数第 j 个字符 B ,反复推演, 可以知道前面的所有小份串的相同位置,都是字符 B 。
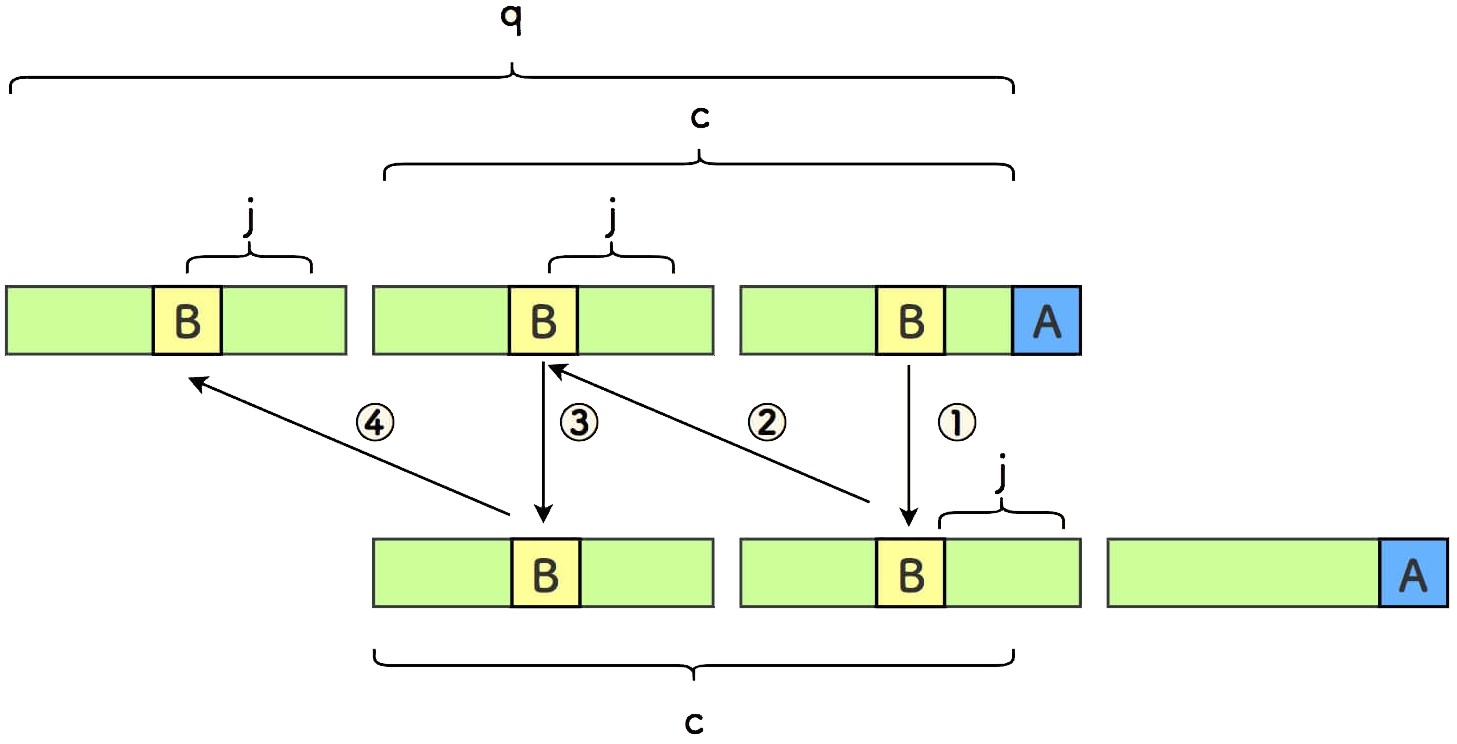
上面的图中:
- ① 号推演,由于上面后缀和下面前缀相等。
- ② 号推演,由于下面的小份串和上面的自身相等。
- 如此,反复进行。
对最后一个小份串上的所有字符, 都会在前面的小份串相同位置重复,那么 s 是一个周期串。
上面推演中的一个细节是,无法推演小份串的倒数第一个字符。
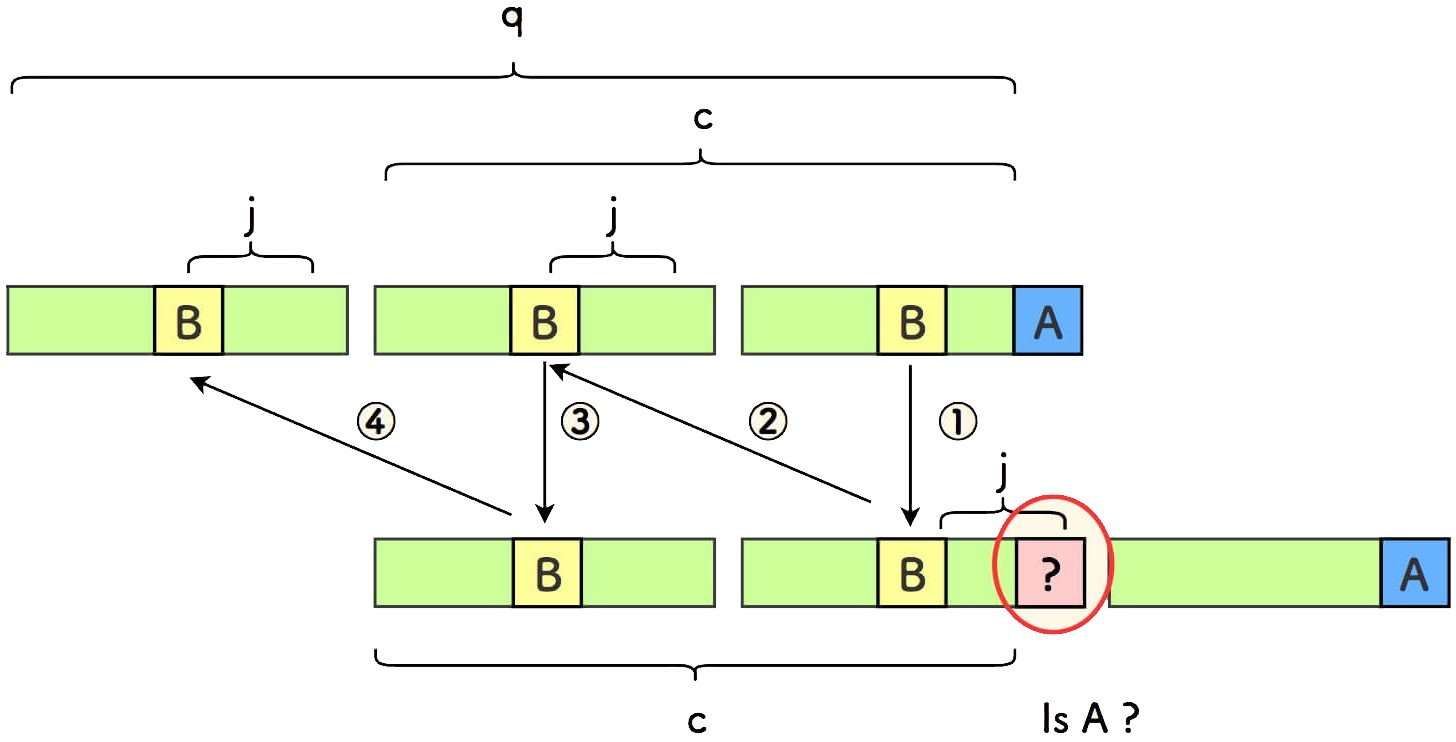
原因在于,尾端字符不在最长前后公共缀的范围内。
细节处理就是,需要判断一次尾巴字符 A 是否和上一个小串对应位置的字符相等。
一旦此细节满足,即可完成整体推演过程,s 就一定是一个周期串。
代码展示
public boolean repeatedSubstringPattern(String s) {
int ls = s.length();
if (ls <= 1) {
return false;
}
int lq = ls - 1;
int[] next = getNext(s);
int lc = next[ls - 1];
if (s.charAt(lc) == s.charAt(ls - 1) && ls % (lq - lc) == 0) {
return true;
}
return false;
}
public int[] getNext(String p) {
// 构建 next 数组,数组长度为匹配串的长度(next 数组是和匹配串相关的)
int lp = p.length();
int[] next = new int[lp];
next[0] = -1;
if (lp > 1) {
next[1] = 0;
//i: 当前要求解next[i]
//m: cn始终记录next[i - 1]的值
int i = 2;
int m = next[i - 1];
while (i < lp) {
if (p.charAt(i - 1) == p.charAt(m)) {// p[m] == p[i-1]
next[i] = m + 1;
i++;
m = next[i - 1];
} else if (m != 0 && p.charAt(i - 1) != p.charAt(m)) {// p[m] != p[i-1]但前后缀还有匹配的可能
m = next[m];
} else if (m == 0 && p.charAt(i - 1) != p.charAt(m)) {// p[m] != p[i-1]且前后缀没有匹配的可能
next[i] = 0;
i++;
}
}
}
return next;
}时间复杂度:O(n)
空间复杂度:O(n)
总结
打基础的时候,不要太迷恋于库函数。
如果库函数仅仅是 解题过程中的一小部分,并且你已经很清楚这个库函数的内部实现原理的话,可以考虑使用库函数。
双指针法在数组,链表和字符串中很常用。
当需要固定规律一段一段去处理字符串的时候,要想想在在 for 循环的表达式上做做文章。
KMP算法是字符串查找最重要的算法
