3.无重复字符的最长子串
难度:中等
给定一个字符串,请你找出其中不含有重复字符的 最长子串 的长度。
示例 1:
输入: "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。示例 2:
输入: "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b",所以其长度为 1。示例 3:
输入: "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke",所以其长度为 3。
请注意,你的答案必须是 子串 的长度,"pwke" 是一个子序列,不是子串。提示:
0 <= s.length <= 5 * 10^(4)s由英文字母、数字、符号和空格组成
解题思路
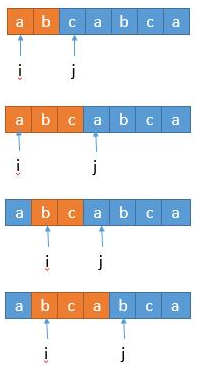
我的思路:
- 设定两个指针 left 和 right,其中 right 负责寻找当前不含有重复字符的最长子串的末尾,left 指向当前当前不含有重复字符的最长子串的开头
- 设定最长字串长度 maxLength,初始为 0
- 设定一个哈希表 map,用来存储从 left 开始,到 right 结束,中间被扫描过的每个字符的位置,显然最长字串中每个字符的出现位置都应该是唯一的
- 起始的时候 left 指向 0,right 往右边扫描
- right 扫描到一个字符 c 的时候,先在哈希表中寻找是否有以 c 为 key 的元素存在:
- 如果哈希表中对应元素 c 存在,且 其位置大于或等于 left,说明从 left 开始不是第一次碰到该字符,此时:
- 更新
left为map.get(c) + 1(即重复字符的下一个位置),以确保窗口中没有重复字符
- 更新
- 如果哈希表中对应元素 c 存在,且 其位置大于或等于 left,说明从 left 开始不是第一次碰到该字符,此时:
- 将当前字符 c 及其位置放入哈希表,这会覆盖相同字符的旧位置
- 使用
right - left + 1计算当前无重复字符子串的长度,并更新maxLength - right == s.length 的时候,退出循环,返回 maxLength
我的代码
public int lengthOfLongestSubstring(String s) {
int left = 0;
int right = 0;
int maxLength = 0;
HashMap<Character, Integer> map = new HashMap<>();
while (right < s.length()) {
char c = s.charAt(right);
if (map.containsKey(c)) {
left = Math.max(map.get(c) + 1, left);
}
map.put(c, right);
maxLength = Math.max(maxLength, right - left + 1);
right++;
}
return maxLength;
}时间复杂度:O(n)
空间复杂度:O(n)
思路来源
这道题主要用到的思路是:滑动窗口
滑动窗口
滑动窗口的思路其实非常简单,就是维护一个窗口,不断滑动,然后更新答案。该算法的大致逻辑如下:
int left = 0, right = 0;
while (left < right && right < s.size()) {
// 增大窗口
window.add(s[right]);
right++;
while (window needs shrink) {
// 缩小窗口
window.remove(s[left]);
left++;
}
}所谓的窗口其实就是一个队列,比如例题中的 abcabcbb,进入这个队列(窗口)为 abc 满足题目要求,当再进入 a,队列变成了 abca,这时候不满足要求了,所以我们要移动这个队列。
其实困扰大家的,不是算法的思路,而是各种细节问题。比如说:如何向窗口中添加新元素,如何缩小窗口,什么时候缩小窗口,在窗口滑动的哪个阶段更新结果合适。
代码模板
/* 滑动窗口算法框架 */
void slidingWindow(String s) {
// 用合适的数据结构记录窗口中的字符及其频率
HashMap<Character, Integer> window = new HashMap<>();
int left = 0, right = 0;
while (right < s.length()) {
// c 是将移入窗口的字符
char c = s.charAt(right);
// 增大窗口
right++;
// 进行窗口内数据的一系列更新
window.put(c, window.getOrDefault(c, 0) + 1);
...
/*** debug 输出的位置 ***/
// 注意在最终的解法代码中不要 print
// 因为 IO 操作很耗时,可能导致超时
System.out.printf("window: [%d, %d)\n", left, right);
/********************/
// 判断左侧窗口是否要收缩
while (window needs shrink) {
// d 是将移出窗口的字符
char d = s.charAt(left);
// 缩小窗口
left++;
// 进行窗口内数据的一系列更新
window.put(d, window.get(d) - 1);
...
}
}
}其中两处 ... 表示的更新窗口数据的地方,到时候我们直接往里面填就行了。
而且,这两个 ... 处的操作分别是扩大和缩小窗口的更新操作,它们的操作其实是完全对称的。
虽然滑动窗口代码框架中有一个嵌套的 while 循环,但因为指针 left, right 不会回退(它们的值只增不减),所以字符串/数组中的每个元素都只会进入窗口一次,然后被移出窗口一次,所以算法的时间复杂度就和字符串/数组的长度成正比,依然是 O(N),其中 N 是输入字符串/数组的长度。
套模板的写法
public int lengthOfLongestSubstring(String s) {
// 用合适的数据结构记录窗口中的字符及其频率
HashMap<Character, Integer> window = new HashMap<>();
int left = 0;
int right = 0;
// 记录结果
int maxLength = 0;
while (right < s.length()) {
// c 是将移入窗口的字符
char c = s.charAt(right);
// 增大窗口
right++;
// 进行窗口内数据的一系列更新
window.put(c, window.getOrDefault(c, 0) + 1);
// 判断左侧窗口是否要收缩
while (window.get(c) > 1) {
// d 是将移出窗口的字符
char d = s.charAt(left);
// 缩小窗口
left++;
// 进行窗口内数据的一系列更新
window.put(d, window.get(d) - 1);
}
// 在这里更新结果
maxLength = Math.max(maxLength, right - left);
}
return maxLength;
}时间复杂度:O(n)
空间复杂度:O(n)
上述代码中,哈希表中存储的是字符及其出现的频率,一旦发现重复字符,就会通过一个 while 循环来不断移动左边界,直到窗口中的重复字符被完全排除,这保证了窗口始终保持无重复字符的状态。
而我的代码中,哈希表中存储的是字符及其出现的最新位置,在发现重复字符时,可以通过一次操作,直接让左边界更新为重复字符的最新出现位置,而不需要像我的代码中的 while 循环那样逐步移动左边界。
从效率的角度来看,我的代码是更优的选择。
其他解法
这里我们可以不用 Hash ,直接用数组来代替。
字符的 ASCII 码值可以作为数组的下标,数组存储该字符所在字符串的位置。
这种方式适用于字符集比较小的情况,因为我们会直接开辟和字符集等大的数组。
public int lengthOfLongestSubstring(String s) {
int length = 0, i = 0, j = 0;
int[] index = new int[128];
while (i < s.length() && j < s.length()) {
char a = s.charAt(j);
if (index[a] != 0 && index[a]> i) {
i = index[a];
}
index[a] = j+1;
length = Math.max(j + 1 - i, length);
j++;
}
return length;
}注意:Java 里定义数组的时候会自动初始化,全部赋值为0,在使用的时候需要多加留意。
时间复杂度:O(n)
空间复杂度:O(m),m 代表字符集的大小。这次不论原字符串多小,都会利用这么大的空间
总结
综上,我们一步一步的寻求可优化的地方,对算法进行了优化。
滑动窗口也可以理解为双指针法的一种,只不过这种解法更像是一个窗口的移动,所以叫做滑动窗口更适合一些。
加深了 Hash 的应用,以及利用数组巧妙的实现了 Hash 的功能。
