700.二叉搜索树中的搜索
难度:容易
给定二叉搜索树(BST)的根节点 root 和一个整数值 val。
你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在,则返回 null 。
示例 1:
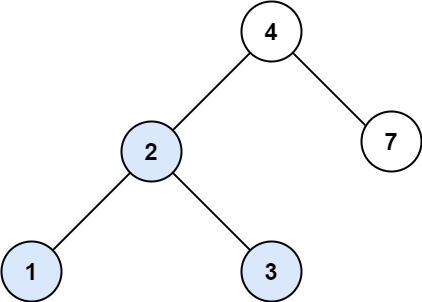
输入:root = [4,2,7,1,3], val = 2
输出:[2,1,3]示例 2:
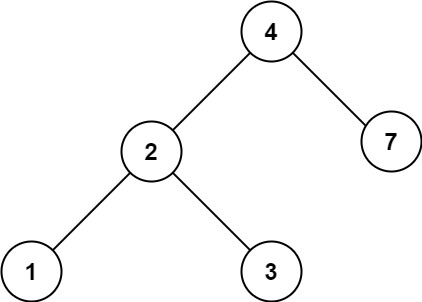
输入:root = [4,2,7,1,3], val = 5
输出:[]提示:
- 树中节点数在
[1, 5000]范围内 1 <= Node.val <= 107root是二叉搜索树1 <= val <= 107
递归法
二叉搜索树是一个有序树:
- 若它的左子树不空,则左子树上所有结点的值都小于它的根结点的值;
- 若它的右子树不空,则右子树上所有结点的值都大于它的根结点的值;
- 它的左、右子树也分别为二叉搜索树
算法步骤:
- 检查当前节点是否为
null:如果当前节点为null,说明已经到达了树的底部而没有找到目标值,因此返回null。 - 比较当前节点的值与目标值:
- 如果目标值等于当前节点的值,那么找到了目标节点,返回当前节点。
- 如果目标值小于当前节点的值,说明目标节点(如果存在)一定在当前节点的左子树中,因此递归地在当前节点的左子树中查找目标值。
- 如果目标值大于当前节点的值,说明目标节点(如果存在)一定在当前节点的右子树中,因此递归地在当前节点的右子树中查找目标值。
- 递归查找:根据目标值与当前节点值的比较结果,选择左子树或右子树进行递归查找。
代码展示
public TreeNode searchBST(TreeNode root, int val) {
if (root == null) {
return null;
} else if (val == root.val) {
return root;
} else if (val < root.val) {
return searchBST(root.left, val);
} else if (val > root.val) {
return searchBST(root.right, val);
}
return null;
}时间复杂度:O(h),其中h是树的高度。在最坏的情况下(即树高度最大时),算法的时间复杂度与树的高度成线性关系。对于一棵平衡的二叉搜索树,时间复杂度是O(log n),其中n是树中节点的数量。对于一棵非平衡的二叉搜索树,最坏情况下的时间复杂度可能达到O(n)。
空间复杂度:O(h),递归调用栈的最大深度等于树的高度h。对于平衡二叉搜索树,空间复杂度是O(log n),对于非平衡二叉搜索树,最坏情况下的空间复杂度是O(n)。
迭代法
一提到二叉树遍历的迭代法,可能立刻想起 使用栈来模拟深度遍历,使用队列来模拟广度遍历。
对于二叉搜索树可就不一样了,因为二叉搜索树的特殊性,也就是节点的有序性,可以不使用辅助栈或者队列就可以写出迭代法。
对于一般二叉树,递归过程中还有回溯的过程,例如走一个左方向的分支走到头了,那么要调头,再走右分支。
而 对于二叉搜索树,不需要回溯的过程,因为节点的有序性已经帮我们确定了搜索的方向。
算法步骤
- 初始化结果节点:首先,定义一个
TreeNode类型的变量result,初始化为null,用于存储查找的结果。 - 检查根节点是否为空:如果传入的根节点
root为空,则直接返回null,表示树中没有节点,因此查找失败。 - 将根节点赋值给结果变量:将
root赋值给result,以便从根节点开始进行查找。 - 迭代查找:使用
while循环不断迭代查找:- 如果
val等于result节点的值,说明已经找到目标节点,跳出循环。 - 如果
val小于result节点的值,说明目标节点(如果存在)位于当前节点的左子树中,因此将result更新为其左子节点,继续迭代。 - 如果
val大于result节点的值,说明目标节点(如果存在)位于当前节点的右子树中,因此将result更新为其右子节点,继续迭代。
- 如果
- 返回结果:循环结束后,
result要么是目标节点(找到目标值),要么是null(未找到目标值)。返回result作为查找结果。
代码展示
public TreeNode searchBST(TreeNode root, int val) {
TreeNode result = null;
if (root == null) {
return result;
}
result = root;
while (result != null) {
if (val == result.val) {
break;
} else if (val < result.val) {
result = result.left;
} else if (val > result.val) {
result = result.right;
}
}
return result;
}时间复杂度:O(h),其中h是树的高度。在最坏的情况下(树高度最大时),算法的时间复杂度与树的高度成线性关系。对于平衡的二叉搜索树,时间复杂度是O(log n),其中n是树中节点的数量。对于非平衡的二叉搜索树,最坏情况下的时间复杂度可能达到O(n)。
空间复杂度:O(1),算法只使用了有限的几个变量,与树的大小和形状无关。
总结
这种迭代方法提供了一种空间效率更高的方式来在二叉搜索树中查找一个值,特别适合于深度较大的树,因为它避免了递归造成的栈空间开销。
