501.二叉搜索树中的众数
难度:简单
给你一个含重复值的二叉搜索树(BST)的根节点 root ,找出并返回 BST 中的所有 众数(即,出现频率最高的元素)。
如果树中有不止一个众数,可以按 任意顺序 返回。
假定 BST 满足如下定义:
- 结点左子树中所含节点的值 小于等于 当前节点的值
- 结点右子树中所含节点的值 大于等于 当前节点的值
- 左子树和右子树都是二叉搜索树
示例 1:
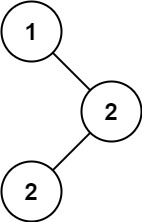
输入:root = [1,null,2,2]
输出:[2]示例 2:
输入:root = [0]
输出:[0]提示:
- 树中节点的数目在范围
[1, 104]内 -105 <= Node.val <= 105
进阶:你可以不使用额外的空间吗?(假设由递归产生的隐式调用栈的开销不被计算在内)
解题思路
二叉搜索树的两大性质:
- 二叉搜索树是一个有序树:
- 若它的左子树不空,则左子树上所有结点的值都小于它的根结点的值;
- 若它的右子树不空,则右子树上所有结点的值都大于它的根结点的值;
- 它的左、右子树也分别为二叉搜索树
- 二叉搜索树的中序遍历结果是一个递增序列
根据性质 2,我们可以知道在二叉搜索树的中序遍历结果中,相等的元素一定是相邻的,这给我们找众数提供了很大遍历。
中序遍历以后,这道题就变成了:在有序序列中寻找众数。
核心逻辑:
- 中序遍历准备:使用一个栈来辅助非递归的中序遍历过程,以及定义
pre(前一个访问的节点)和cur(当前访问的节点)变量来跟踪遍历。同时,维护curCount(当前值的出现次数)和maxCount(迄今为止的最大出现次数)来记录出现频率。 - 中序遍历执行:遵循中序遍历的顺序,首先遍历到每个节点的最左子节点。
- 对于每个节点,如果是第一个节点或者当前节点与前一个节点值不同,则重置
curCount为 1 - 如果当前节点与前一个节点值,增加
curCount
- 对于每个节点,如果是第一个节点或者当前节点与前一个节点值不同,则重置
- 众数更新逻辑:
- 如果当前计数
curCount大于最大计数maxCount,清空结果列表 并添加当前值,同时更新maxCount。 - 如果
curCount等于maxCount,直接将当前值加入结果列表。 - 上述操作确保了结果列表始终包含所有的众数。
- 如果当前计数
- 遍历完成后的处理:将累积的众数列表转换成数组格式返回。
代码展示
java
public int[] findMode(TreeNode root) {
// 存储结果的列表
List<Integer> ans = new ArrayList<>();
// 用于中序遍历的栈
Deque<TreeNode> stack = new LinkedList<>();
// 上一个访问的节点
TreeNode pre = null;
// 当前访问的节点
TreeNode cur = root;
// 当前众数的出现次数和当前值的出现次数
int maxCount = 0;
int curCount = 0;
// 中序遍历
while (cur != null || !stack.isEmpty()) {
// 遍历到最左边
while (cur != null) {
stack.push(cur);
cur = cur.left;
}
cur = stack.pop();
// 如果是第一个节点或者当前节点与前一个节点值不同
if (pre == null || pre.val != cur.val) {
curCount = 1;
} else {
// 如果当前节点与前一个节点值相同
curCount++;
}
// 更新结果列表
if (curCount > maxCount) {
ans.clear();
ans.add(cur.val);
maxCount = curCount;
} else if (curCount == maxCount) {
ans.add(cur.val);
}
// 更新前一个节点为当前节点,移动到右子树继续遍历
pre = cur;
cur = cur.right;
}
// 将结果列表转换为数组并返回
return ans.stream().mapToInt(Integer::intValue).toArray();
}时间复杂度:O(n),其中 n 是二叉树的节点数。每一个节点恰好被遍历一次。
空间复杂度:O(h),其中h是树的高度。在最坏的情况下,栈中可能需要存储与树的高度相当数量的节点。对于一棵平衡二叉树,空间复杂度是O(log n),而对于非平衡二叉树,最坏情况下的空间复杂度可能达到O(n)。
总结
二叉搜索树的两大性质:
- 二叉搜索树是一个有序树:
- 若它的左子树不空,则左子树上所有结点的值都小于它的根结点的值;
- 若它的右子树不空,则右子树上所有结点的值都大于它的根结点的值;
- 它的左、右子树也分别为二叉搜索树
- 二叉搜索树的中序遍历结果是一个递增序列
