110.平衡二叉树

难度：容易

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：

一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。

示例 1：

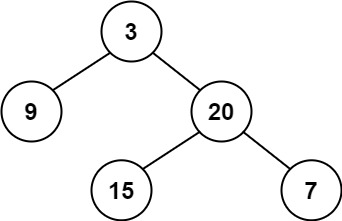
输入：root = [3,9,20,null,null,15,7]
输出：true

示例 2：

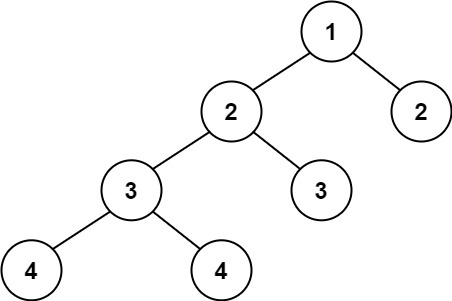
输入：root = [1,2,2,3,3,null,null,4,4]
输出：false

示例 3：

输入：root = []
输出：true

提示：

树中的节点数在范围 [0, 5000] 内
-104 <= Node.val <= 104

解题思路

这道题目和 104.二叉树的最大深度 很像，其实有很大区别。

二叉树的深度 = Max( 左子树的深度 , 右子树的深度 ) +1。

这里我们可以通过递归的方式判断一个二叉树是否平衡。

首先递归地检查所有子树是否平衡，如果左子树或右子树有一个不平衡，则整个树不平衡，函数返回false
若子树平衡，则对于每个节点，递归地计算当前节点的左子树和右子树的深度，取两者的最大值，然后加1（加的这个1代表当前节点本身），以此作为当前节点的树深度。
比较其左右子树的深度差，以确定整棵树是否平衡。

代码展示

java

public boolean isBalanced(TreeNode root) {
    if (root == null) {
        return true;
    }
    // 判断左右子树是否平衡
    if (!isBalanced(root.left) || !isBalanced(root.right)) {
        return false;
    }
    int leftDepth, rightDepth;
    leftDepth = getTreeDepth(root.left);
    rightDepth = getTreeDepth(root.right);
    // 判断当前树是否平衡
    return Math.abs(leftDepth - rightDepth) <= 1;
}

public int getTreeDepth(TreeNode root) {
    if (root == null) {
        return 0;
    }
    return Math.max(getTreeDepth(root.left), getTreeDepth(root.right)) + 1;
}

时间复杂度：O(n^2)，对于isBalanced函数，它在最坏情况下会访问树中的每个节点并计算其深度，这导致了一个高时间复杂度。具体来说，由于getTreeDepth函数对于每个节点都会被调用，整体时间复杂度为O(n^2)，其中n是树中节点的数量。这是因为对于每个节点，都进行了一次深度的计算，而深度计算本身是递归进行的。

空间复杂度：O(n)，空间复杂度主要由递归调用栈的深度决定，在最坏情况下（即树完全不平衡时）空间复杂度为O(n)。

优化写法（从底至顶）

尽管上述方法直观且易于实现，但在效率上可能不是最优的，尤其是对于较大的树。

原因是 重复计算深度：在检查每个节点是否平衡时（即左右子树的深度差是否不超过1），原始方法首先递归地检查左右子树是否各自平衡，然后再分别计算左右子树的深度。这意味着对于每个节点，其子树的深度可能被重复计算多次：一次是在检查子树本身是否平衡时，另一次是在计算当前节点的左右子树深度差时。因为getTreeDepth函数是独立调用的，所以每次调用都会遍历整个子树来计算深度，这导致了大量的重复遍历和计算。

优化这个算法的一个方法是在计算深度的同时检查平衡性，从而避免重复的深度计算。

在这个优化版本中，getDepth 函数不仅计算树的深度，还检查树是否平衡：

如果遇到不平衡的子树，即左右子树的深度差大于1，getDepth 函数会提前返回-1。这个返回值作为一个信号，表示树在当前节点或其子树中已经不平衡。
在递归调用 getDepth 函数时，如果返回值为-1，表示找到了不平衡的子树，这时不需要继续计算深度，而是直接传递这个信号向上返回。
isBalanced 函数现在只需要检查 getDepth 函数的返回值是否为-1即可。如果是-1，表示树不平衡；否则，树平衡。

代码展示

java

public boolean isBalanced(TreeNode root) {
    return getDepth(root) != -1;
}

private int getDepth(TreeNode node) {
    if (node == null) {
        return 0;
    }
    int leftDepth = getDepth(node.left);
    if (leftDepth == -1) {// 左子树不平衡
        return -1; 
    }
    int rightDepth = getDepth(node.right);
    if (rightDepth == -1) {// 右子树不平衡
        return -1; 
    }
    if (Math.abs(leftDepth - rightDepth) > 1) {// 当前节点不平衡
        return -1; 
    }
    return Math.max(leftDepth, rightDepth) + 1; // 返回当前节点的深度
}

时间复杂度：O(n)，其中 n 是二叉树的节点数。每一个节点恰好被遍历一次。

空间复杂度：O(n)，空间复杂度主要取决于递归调用栈的深度，最坏情况下（树完全不平衡时）为O(n)，最好情况下（树完全平衡时）为O(log n)。

总结

平衡二叉树的每一个子树都是平衡二叉树。

110.平衡二叉树 ​

解题思路 ​

代码展示 ​

优化写法（从底至顶） ​

代码展示 ​

总结 ​

110.平衡二叉树

解题思路

代码展示

优化写法（从底至顶）

代码展示

总结