144.二叉树的前序遍历
难度:容易
给你二叉树的根节点 root ,返回它节点值的 前序 遍历。
示例 1:
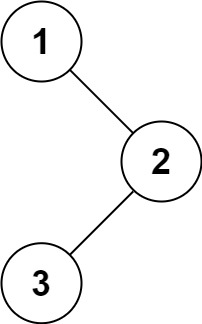
输入:root = [1,null,2,3]
输出:[1,2,3]示例 2:
输入:root = []
输出:[]示例 3:
输入:root = [1]
输出:[1]示例 4:
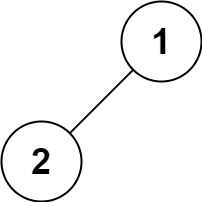
输入:root = [1,2]
输出:[1,2]示例 5:
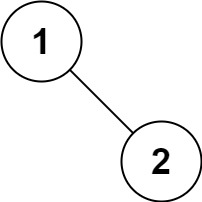
输入:root = [1,null,2]
输出:[1,2]提示:
- 树中节点数目在范围
[0, 100]内 -100 <= Node.val <= 100
**进阶:**递归算法很简单,你可以通过迭代算法完成吗?
递归算法
递归算法的三个要素:
- 确定递归函数的参数和返回值: 确定哪些参数是递归的过程中需要处理的,那么就在递归函数里加上这个参数, 并且还要明确每次递归的返回值是什么,从而确定递归函数的返回类型。
- 确定终止条件: 写完递归算法,在运行的时候,经常会遇到栈溢出的错误,这是因为 终止条件 写的不对,操作系统也是用一个栈的结构来保存每一层递归的信息,如果递归没有终止,操作系统的内存栈必然就会溢出。
- 确定单层递归的逻辑: 确定每一层递归需要处理的信息。在这里也就会重复调用自己来实现递归的过程。
每次写递归,都按照这三要素来写,可以保证写出正确的递归算法!
以前序遍历为例:
确定递归函数的参数和返回值:因为要打印出前序遍历节点的数值,所以参数里需要传入
result来放节点的数值,除了这一点就不需要再处理什么数据了也不需要有返回值,所以递归函数返回类型就是void,代码如下:javavoid preorder(TreeNode root, List<Integer> result)确定终止条件:在递归的过程中,如何算是递归结束了呢,当然是当前遍历的节点为空,那么本层递归就要结束了,所以如果当前遍历的这个节点是空,就直接
return,代码如下:javaif (root == null) { return; }确定单层递归的逻辑:前序遍历是中左右的循序,所以在单层递归的逻辑,要先取中节点的数值,代码如下:
javaresult.add(root.val); // 中 preorder(root.left, result); // 左 preorder(root.right, result); // 右
单层递归的逻辑就是按照中左右的顺序来处理的,这样二叉树的前序遍历,基本就写完了。
代码展示
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> result = new ArrayList<>();
preorder(root, result);
return result;
}
public void preorder(TreeNode root, List<Integer> result) {
if (root == null) {
return;
}
result.add(root.val);
preorder(root.left, result);
preorder(root.right, result);
}时间复杂度:O(n),其中 n 是二叉树的节点数。每一个节点恰好被遍历一次。
空间复杂度:O(n),为递归过程中栈的开销,平均情况下为 O(logn),最坏情况下树呈现链状,为 O(n)。
迭代法
递归的实现就是:每一次递归调用都会把函数的局部变量、参数值和返回地址等压入调用栈中,然后递归返回的时候,从栈顶弹出上一次递归的各项参数,所以这就是递归可以返回上一层位置的原因。
那么我们也可以用迭代的方式实现递归函数,两种方式是等价的,区别在于递归的时候隐式地维护了一个栈,而我们在迭代的时候需要显式地将这个栈模拟出来,其余的实现与细节都相同。
代码原理:
- 创建辅助栈和结果列表: 定义一个栈
stack用于存放将要访问的节点,和一个列表result用于存储遍历的结果。 - 初始化栈: 如果根节点
root不为null,将它压入栈中。 - 迭代遍历: 使用一个
while循环来迭代遍历树,只要栈不为空,就继续循环。 - 访问节点: 在每次循环中,从栈中弹出一个节点,将它的值添加到结果列表中。
- 压入右孩子和左孩子: 如果弹出节点的右孩子存在,将右孩子压入栈中。然后,如果左孩子存在,也将左孩子压入栈中。这样做是因为栈是后进先出的结构,我们希望先处理左孩子,所以左孩子后压入栈。
通过这种方式,算法首先访问根节点,然后是左子树,最后是右子树,正好符合前序遍历的顺序(根-左-右)。使用栈来存储未来将要访问的节点,从而实现了迭代遍历,而不是使用递归。
代码展示
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> result = new ArrayList<>();
Deque<TreeNode> stack = new LinkedList<>();
if (root == null) {
return result;
}
stack.push(root);
while (!stack.isEmpty()) {
TreeNode node = stack.pop();
result.add(node.val);
// 因为栈是后进先出,所以先压入右孩子
if (node.right != null) {
stack.push(node.right);
}
// 后压入左孩子
if (node.left != null) {
stack.push(node.left);
}
}
return result;
}时间复杂度:O(n),其中 n 是二叉树的节点数。每一个节点恰好被遍历一次。
空间复杂度:O(n),为迭代过程中显式栈的开销,平均情况下为 O(logn),最坏情况下树呈现链状,为 O(n)。
总结
迭代法比递归法更难想到。
