111.二叉树的最小深度
难度:容易
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
**说明:**叶子节点是指没有子节点的节点。
示例 1:
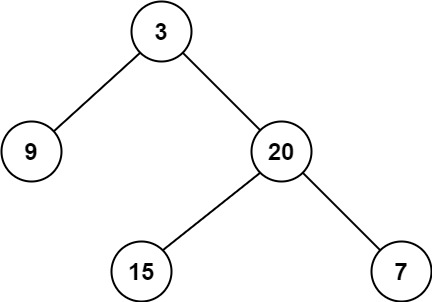
输入:root = [3,9,20,null,null,15,7]
输出:2示例 2:
输入:root = [2,null,3,null,4,null,5,null,6]
输出:5提示:
- 树中节点数的范围在
[0, 10^5]内 -1000 <= Node.val <= 1000
层序遍历+队列法
这道题和 104 题非常类似,要点是:当左右孩子都为空的时候,说明遍历到最小深度了。
层序遍历一个二叉树。就是从左到右、一层一层地去遍历二叉树。这种遍历的方式需要借用一个辅助数据结构即队列来实现。
队列具有 先进先出 的特性,符合层序遍历的逻辑。这种层序遍历的方式就是图论中的广度优先遍历,只不过我们应用在了二叉树上。
算法流程:
- 处理特例:若根节点为空,则返回 0
- 根节点入队
- BFS 循环: 判断队列是否为空。如果不为空,说明还有节点需要遍历
- 初始化当前层的节点个数
currentLevelSize为队列的大小。 - 深度增加。
- 使用一个内层循环,遍历当前层的节点。循环次数为当前层的节点个数
currentLevelSize。- 如果当前节点没有左、右子节点,说明找到最小深度了,直接返回深度值。
- 如果当前节点有左子节点,将左子节点入队。
- 如果当前节点有右子节点,将右子节点入队。
- 此时队列中已经把当前层的节点都出队了,同时把下一层的节点都入队了,因此队列大小刚好变成了下一层的节点个数。
- 初始化当前层的节点个数
- 返回深度值:这一步其实没什么必要了,BFS 循环里一定会提前返回深度值的。
代码展示
java
public int minDepth(TreeNode root) {
// 若根节点为空,则返回0
if (root == null) {
return 0;
}
int depth = 0;
Deque<TreeNode> queue = new LinkedList<>();
// 根节点入队
queue.add(root);
// BFS 循环
while (!queue.isEmpty()) {
int currentLayerSize = queue.size();
// 深度增加
depth++;
// 这里一定要使用固定大小currentLayerSize,不要使用queue.size(),因为queue不停地出队入队,所以其大小是不断变化的
for (int i = 0; i < currentLayerSize; i++) {
TreeNode current = queue.poll();
if (current.left == null && current.right == null) {
return depth;
}
if (current.left != null) {
queue.add(current.left);
}
if (current.right != null) {
queue.add(current.right);
}
}
}
return 0;
}时间复杂度:O(n),其中 n 是二叉树的节点数。每一个节点恰好被遍历一次。
空间复杂度:O(n),最差情况下,即当树为满二叉树时,最多有 (n+1)/2 个树节点 同时 在 queue 中,故使用 O(n) 大小的额外空间。
递归法
使用递归法求二叉树的最小深度与求最大深度有所不同。
二叉树的最小深度是从根节点到最近的叶子节点的最短路径上的节点数。
这里的关键是要注意,叶子节点是指没有子节点的节点。
因此,在计算最小深度时,如果某个节点只有一个子节点,我们不能简单地取左右子树深度的最小值,因为没有子节点的那一侧实际上并不构成一条到叶子节点的路径。
代码展示
java
public int maxDepth(TreeNode root) {
// 如果当前节点为空,意味着深度为0
if (root == null) {
return 0;
}
// 递归求左子树的最小深度
int leftDepth = minDepth(root.left);
// 递归求右子树的最小深度
int rightDepth = minDepth(root.right);
// 如果左子树或右子树有一个为空,最小深度为非空子树的最小深度 + 1
if (root.left == null || root.right == null) {
return leftDepth + rightDepth + 1;
}
// 如果左右子树都不为空,最小深度为左右子树最小深度的最小值 + 1
return Math.min(leftDepth, rightDepth) + 1;
}时间复杂度:O(n),其中 n 是二叉树的节点数。每一个节点恰好被遍历一次。
空间复杂度:O(1),因为这种做法没有使用队列,所以大大降低了空间复杂度。
总结
这份代码可以作为二叉树层序遍历的模板。
