654.最大二叉树
难度:中等
给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:
- 创建一个根节点,其值为
nums中的最大值。 - 递归地在最大值 左边 的 子数组前缀上 构建左子树。
- 递归地在最大值 右边 的 子数组后缀上 构建右子树。
返回 nums 构建的 最大二叉树 。
示例 1:
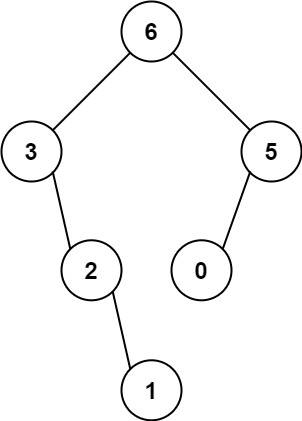
输入:nums = [3,2,1,6,0,5]
输出:[6,3,5,null,2,0,null,null,1]
解释:递归调用如下所示:
- [3,2,1,6,0,5] 中的最大值是 6 ,左边部分是 [3,2,1] ,右边部分是 [0,5] 。
- [3,2,1] 中的最大值是 3 ,左边部分是 [] ,右边部分是 [2,1] 。
- 空数组,无子节点。
- [2,1] 中的最大值是 2 ,左边部分是 [] ,右边部分是 [1] 。
- 空数组,无子节点。
- 只有一个元素,所以子节点是一个值为 1 的节点。
- [0,5] 中的最大值是 5 ,左边部分是 [0] ,右边部分是 [] 。
- 只有一个元素,所以子节点是一个值为 0 的节点。
- 空数组,无子节点。示例 2:
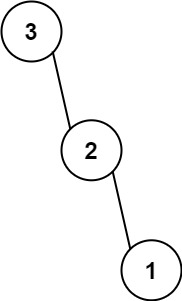
输入:nums = [3,2,1]
输出:[3,null,2,null,1]提示:
1 <= nums.length <= 10000 <= nums[i] <= 1000nums中的所有整数 互不相同
解题思路
最简单的方法是直接按照题目描述进行模拟。
我们用递归函数 construct(int[] nums, int beginIndex, int endIndex) 表示对数组 nums 中从 nums[beginIndex] 到 nums[endIndex] 的元素构建一棵树。
首先找到这一区间中的最大值,记为
nums[maxIndex],这样就确定了根节点的值,随后递归构建左子树和右子树。左子树为
construct(nums, beginIndex, maxIndex - 1)右子树为
construct(nums, maxIndex + 1, endIndex)当递归到一个无效的区间(即
beginIndex > endIndex)时,便可以返回一棵空的树
代码展示
public TreeNode constructMaximumBinaryTree(int[] nums) {
return construct(nums, 0, nums.length - 1);
}
public TreeNode construct(int[] nums, int beginIndex, int endIndex) {
// 当前树为空
if (beginIndex > endIndex) {
return null;
}
// 在数组中找到根节点的位置,确定左右子树的范围
int maxIndex = beginIndex;
for (int i = beginIndex + 1; i <= endIndex; i++) {
if (nums[i] > nums[maxIndex]) {
maxIndex = i;
}
}
// 创建根节点
TreeNode root = new TreeNode(nums[maxIndex]);
// 递归构建左子树和右子树
root.left = construct(nums, beginIndex, maxIndex - 1);
root.right = construct(nums, maxIndex + 1, endIndex);
return root;
}时间复杂度:O(n^2),最坏情况下,对于每个节点,都需要在数组中进行一次线性搜索来找到根节点,这导致了 O(n) 的搜索时间复杂度。由于这个搜索过程对于树中的每个节点都要执行一次,总的时间复杂度为 O(n^2)。
空间复杂度:O(n),主要消耗在递归调用栈上。在最坏的情况下,这个栈的深度与树的高度相同。对于平衡二叉树,高度大约为logn,因此空间复杂度为O(logn)。
总结
递归的边界条件需要细心处理。
注意类似用数组构造二叉树的题目,每次分隔尽量不要定义新的数组,而是通过下标索引直接在原数组上操作,这样可以节约时间和空间上的开销。
一般情况来说:如果让空节点(空指针)进入递归,就不加 if,如果不让空节点进入递归,就加 if 限制一下, 终止条件也会相应的调整。
