404.左叶子之和
难度:容易
给定二叉树的根节点 root ,返回所有左叶子之和。
示例 1:
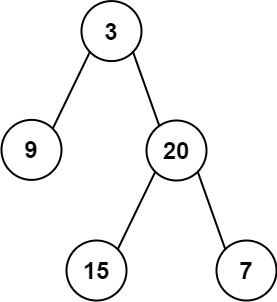
输入: root = [3,9,20,null,null,15,7]
输出: 24
解释: 在这个二叉树中,有两个左叶子,分别是 9 和 15,所以返回 24示例 2:
输入: root = [1]
输出: 0提示:
- 节点数在
[1, 1000]范围内 -1000 <= Node.val <= 1000
递归法
首先要明确一点,什么样的节点是左叶子节点?
比如示例 1 中的9、15、7这三个节点由于没有子节点,所以我们知道他们是叶子节点,但只有9和15是左叶子节点,7并不是左叶子节点,这是怎么判断的呢?
显然,只根据当前节点来判断当前节点是不是左叶子是做不到的,必须要通过该节点的父节点来判断其左孩子是不是左叶子。
若节点 A 的左孩子不为空,且左孩子的左右孩子都为空(说明是叶子节点),那么 A 节点的左孩子就是左叶子节点。
核心判断代码:
if(root.left!=null&&root.left.left==null&&root.left.right==null){
左叶子节点处理逻辑
}递归三部曲:
确定递归函数的参数和返回值
判断一个树的左叶子节点之和,那么一定要传入树的根节点,递归函数的返回值为数值之和,所以返回值为 int
javaint sumOfLeftLeaves(TreeNode root);确定终止条件
如果遍历到空节点,那么其左叶子值一定是 0
javaif (root == NULL) { return 0; }注意,只有当前遍历的节点是父节点,才能判断其子节点是不是左叶子。 所以如果当前遍历的节点是叶子节点,那其左叶子也必定是0,那么终止条件为:
确定单层递归的逻辑
当遇到左叶子节点的父节点的时候,记录其左叶子节点的数值,然后通过递归求取该父节点的右孩子左叶子之和,并相加。
当遇到非左叶子节点的父节点的时候,递归计算其左右孩子的左叶子节点之和,相加便是整个树的左叶子之和。
代码展示
public int sumOfLeftLeaves(TreeNode root){
if(root==null){
return 0;
}
// 检查当前节点是否为左叶子节点的父节点
if(root.left!=null&&root.left.left==null&&root.left.right==null){
return root.left.val+sumOfLeftLeaves(root.right);
}
return sumOfLeftLeaves(root.left)+sumOfLeftLeaves(root.right);
}时间复杂度:O(n),每个节点在递归过程中只被访问一次
空间复杂度:O(h),其中h是树的高度,代表递归调用栈的最大深度。对于平衡二叉树,高度h大约是logn,所以空间复杂度是O(logn) 。但在最坏的情况下(比如树完全不平衡,形成链表状),空间复杂度可以退化到O(n)
层序遍历+迭代法
可以使用层序遍历的迭代方式来模拟递归的过程:
- 初始化:先初始化结果变量
result为0,用于累加左叶子节点的值。 - 空树检查:如果根节点
root为空,则直接返回0,表示没有左叶子节点。 - 队列初始化:创建一个队列
queue,并将根节点root加入队列。这个队列用于按照广度优先的方式遍历树的每个节点。 - 广度优先搜索(BFS):使用一个循环,当队列不为空时,从队列中移除(或“弹出”)当前节点。对于每个节点,算法执行以下操作:
- 左叶子节点检查 :检查当前节点的左子节点是否是一个叶子节点(即,它存在且没有左右子节点)。如果是,将该左叶子节点的值加到
result上。 - 子节点入队:如果当前节点的左子节点存在,将它加入队列以便后续遍历。同样地,如果右子节点存在,也将它加入队列。
- 左叶子节点检查 :检查当前节点的左子节点是否是一个叶子节点(即,它存在且没有左右子节点)。如果是,将该左叶子节点的值加到
- 返回结果:当队列为空,即遍历完树的所有节点后,循环结束。此时
result包含了所有左叶子节点的值之和,将其返回。
关键点:
- 使用队列实现BFS:这种方法利用队列先进先出的特性来实现树的层序遍历(广度优先搜索),这样可以按照从上到下、从左到右的顺序访问树的每个节点。
- 左叶子节点的判断:通过检查一个节点的左子节点是否存在且该左子节点没有自己的子节点来确定它是否为左叶子节点。
代码展示
public int sumOfLeftLeaves(TreeNode root){
int result=0;
// 若根节点为空,则返回0
if(root==null){
return result;
}
Deque<TreeNode> queue=new LinkedList<>();
// 根节点入队
queue.add(root);
// BFS 循环
while(!queue.isEmpty()){
TreeNode current=queue.poll();
// 检查当前节点是否为左叶子节点的父节点
if(current.left!=null&¤t.left.left==null&¤t.left.right==null){
result+=current.left.val;
}
if(current.left!=null){
queue.add(current.left);
}
if(current.right!=null){
queue.add(current.right);
}
}
return result;
}时间复杂度:O(n),其中N是树中节点的数量。算法访问了树的每个节点恰好一次。
空间复杂度:O(n),在最坏的情况下(例如完全二叉树),队列中可能同时包含约N/2个节点,即树的最后一层节点数。因此,空间复杂度取决于队列中最多节点的数量。
总结
这道题目要求左叶子之和,其实是比较绕的,因为不能判断本节点是不是左叶子节点,此时就要通过节点的父节点来判断其左孩子是不是左叶子了。
平时我们解二叉树的题目时,已经习惯了通过节点的左右孩子判断本节点的属性,而本题我们要通过节点的父节点判断本节点的属性。
