559.N叉树的最大深度

难度：容易

给定一个 N 叉树，找到其最大深度。

最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。

N 叉树输入按层序遍历序列化表示，每组子节点由空值分隔（请参见示例）。

示例 1：

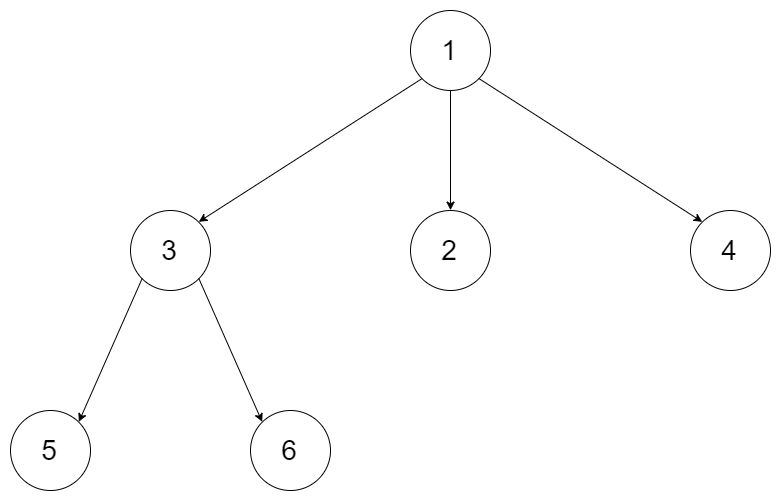
输入：root = [1,null,3,2,4,null,5,6]
输出：3

示例 2：

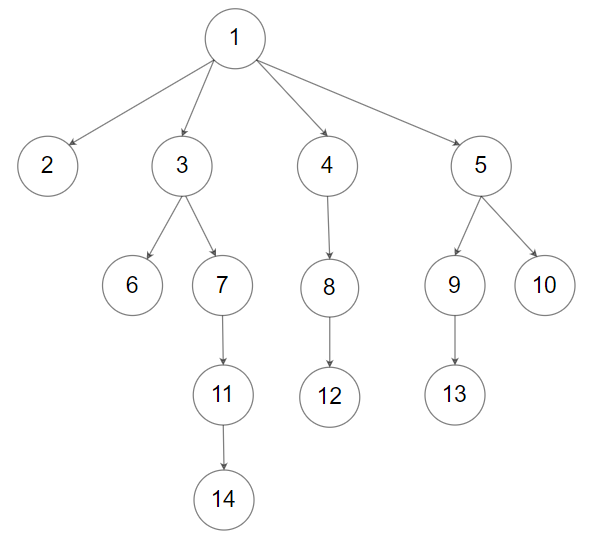
输入：root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
输出：5

提示：

• 树的深度不会超过 1000 。
• 树的节点数目位于 [0, 104] 之间。

层序遍历+队列法

这道题和 102 题非常类似，只不过在单层遍历的时候记录一下当前深度就可以了。

层序遍历一个二叉树。就是从左到右、一层一层地去遍历二叉树。这种遍历的方式需要借用一个辅助数据结构即队列来实现。

队列具有 先进先出 的特性，符合层序遍历的逻辑。这种层序遍历的方式就是图论中的广度优先遍历，只不过我们应用在了二叉树上。

算法流程：

1. 处理特例：若根节点为空，则返回 0
2. 根节点入队
3. BFS 循环： 判断队列是否为空。如果不为空，说明还有节点需要遍历

   1. 初始化当前层的节点个数 currentLevelSize 为队列的大小。

   2. 深度增加。

   3. 使用一个内层循环，遍历当前层的节点。循环次数为当前层的节点个数 currentLevelSize。

      1. 如果当前节点有子节点，将子节点入队。

   4. 此时队列中已经把当前层的节点都出队了，同时把下一层的节点都入队了，因此队列大小刚好变成了下一层的节点个数。

4. 返回深度值：当所有层都遍历完毕后，此时得到的深度值代表的就是最深的那一层。

代码展示

public int maxDepth(Node root) {
    // 若根节点为空，则返回0
    if (root == null) {
        return 0;
    }
    int depth = 0;
    Deque<Node> queue = new LinkedList<>();
    // 根节点入队
    queue.add(root);
    // BFS 循环
    while (!queue.isEmpty()) {
        int currentLayerSize = queue.size();
        // 深度增加
        depth++;
        // 这里一定要使用固定大小currentLayerSize，不要使用queue.size()，因为queue不停地出队入队，所以其大小是不断变化的
        for (int i = 0; i < currentLayerSize; i++) {
            Node current = queue.poll();
            if (current.children != null) {
                queue.addAll(current.children);
            }
        }
    }
    return depth;
}

class Node {
    public int val;
    public List<Node> children;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, List<Node> _children) {
        val = _val;
        children = _children;
    }
};

时间复杂度：O(n)，其中 n 是二叉树的节点数。每一个节点恰好被遍历一次。

空间复杂度：O(n)，最差情况下，即当树为满二叉树时，最多有 (n+1)/2 个树节点 同时 在 queue 中，故使用 O(n) 大小的额外空间。

递归法

递归法的核心思想是，N叉树的最大深度等于其子树深度的最大值加一（加的这个一代表根节点本身）。

代码展示

public int maxDepth(Node root) {
    // 如果当前节点为空，意味着深度为0
    if (root == null) {
        return 0;
    }
    List<Node> children = root.children;
    // 递归求子树的深度
    int maxChildrenDepth = 0;
    for (int i = 0; i < children.size(); i++) {
        maxChildrenDepth = Math.max(maxChildrenDepth, maxDepth(children.get(i)));
    }
    // 当前树的最大深度为子树深度的最大值 + 1（根节点自身）
    return maxChildrenDepth + 1;
}

时间复杂度：O(n)，其中 n 是二叉树的节点数。每一个节点恰好被遍历一次。

空间复杂度：O(1)，因为这种做法没有使用队列，所以大大降低了空间复杂度。

总结

这份代码可以作为二叉树层序遍历的模板。