113.路径总和Ⅱ
难度:中等
给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。
叶子节点 是指没有子节点的节点。
示例 1:
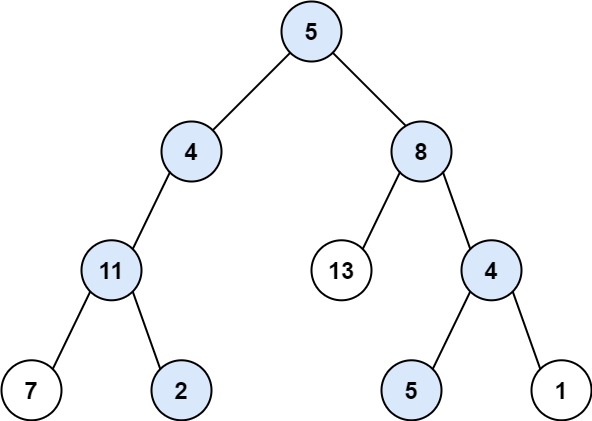
输入:root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出:[[5,4,11,2],[5,8,4,5]]示例 2:
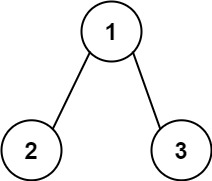
输入:root = [1,2,3], targetSum = 5
输出:[]示例 3:
输入:root = [1,2], targetSum = 0
输出:[]提示:
- 树中节点总数在范围
[0, 5000]内 -1000 <= Node.val <= 1000-1000 <= targetSum <= 1000
前序遍历+递归+回溯法
联想 257.二叉树的所有路径 题,我们可以想到使用前序遍历的方式,记录从根节点到当前节点的路径和。
算法步骤:
- 初始化结果集:创建一个列表
result用于存储所有符合条件的路径。 - 空树检查:如果根节点
root为空,则直接返回空的结果集。 - 递归遍历树:使用
preorder函数递归地遍历树,同时传递当前路径currentPath、目标和targetSum和结果集result作为参数。
preorder方法:
- 终止条件:如果当前节点为空,即到达了叶子节点的子节点,函数直接返回。
- 路径更新:将当前节点的值添加到
currentPath中。这代表当前节点被包含在路径中。 - 叶子节点检查:如果当前节点是叶子节点(即没有左右子节点),并且节点值等于剩余的
targetSum(意味着这是一条满足条件的路径),则将currentPath的一个深拷贝添加到结果集中。这里使用深拷贝是因为currentPath会随着递归的进行而不断变化,我们需要保存当前状态的快照。 - 递归子节点:对左右子节点递归调用
preorder函数,将targetSum减去当前节点的值,因为这部分和已经由当前路径覆盖。这样可以确保只有当整条路径的和等于原始targetSum时,路径才会被添加到结果集中。 - 回溯:在探索完当前节点的所有子路径后,从
currentPath中移除当前节点的值,以恢复到探索当前节点之前的状态。这一步是算法回溯的关键,它确保了在返回上一层递归时currentPath反映的是正确的路径状态。
关键点:
- 深度优先搜索与回溯:算法结合了DFS和回溯的策略,通过递归遍历树的每个节点,并在每一步中尝试所有可能的路径。当路径不满足条件或已经探索完毕时,算法通过回溯步骤撤销当前的选择,尝试其他可能性。
- 路径的动态构建:
currentPath在递归过程中不断更新,它反映了从根节点到当前节点的路径。这种动态构建路径的方式使得算法能够有效地记录和更新探索状态。
代码展示
java
public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
List<List<Integer>> result = new ArrayList<>();
if (root == null) {
return result;
}
List<Integer> currentPath = new ArrayList<>();
preorder(root, currentPath, targetSum, result);
return result;
}
public void preorder(TreeNode root, List<Integer> currentPath, int targetSum, List<List<Integer>> result) {
if (root == null) {
return;
}
int pathSize = currentPath.size(); // 记录进入这个节点前路径的长度
currentPath.add(root.val);
if (root.left == null && root.right == null && root.val == targetSum) {// 如果是叶子节点,并且找到了目标路径
// 深拷贝,规避Java的引用传递的特性
List<Integer> temp = new ArrayList<>(currentPath);
result.add(temp);
} else {// 非叶子节点或者是叶子节点但没找到目标路径,递归遍历
preorder(root.left, currentPath, targetSum - root.val, result);
preorder(root.right, currentPath, targetSum - root.val, result);
}
currentPath.remove(pathSize);// 恢复路径到进入这个节点前的状态
}时间复杂度:O(n),其中n是树中节点的数量。算法需要访问树中的每个节点来判断路径是否符合条件。
空间复杂度:O(n),最坏情况下(当树完全不平衡时),递归调用栈的深度可以达到n。此外,如果每个节点都在一条符合条件的路径上,那么存储这些路径需要的空间也是O(n)。对于平衡二叉树,空间复杂度为O(logn),因为递归调用栈的深度由树的高度决定。
前序遍历+栈+回溯法
联想 257.二叉树的所有路径 题,我们可以想到使用前序遍历的方式,记录从根节点到当前节点的路径和。
这样我们使用两个栈:一个用于存储节点(nodeStack),另一个用于存储到当前节点为止的路径和(pathSumStack)
算法步骤:
- 初始化结果集:创建一个
result列表,用于存储所有满足条件的路径。 - 边界条件处理:如果根节点为空,则直接返回空的结果集。
- 栈的初始化:初始化三个栈 —
nodeStack用于存储遍历过程中的节点,pathSumStack用于跟踪到当前节点为止的路径和,pathStack用于存储构成当前路径和的节点值列表。 - 迭代遍历:在栈非空的条件下,循环执行以下步骤:
- 从各个栈中弹出当前节点、当前路径和、当前路径列表。
- 如果当前节点是叶子节点(即没有子节点)且当前路径和等于目标和,则将当前路径列表深拷贝到结果集中。
- 对于当前节点的右子节点和左子节点(如果存在),更新路径和并将新的路径和、新的路径列表及子节点推入相应的栈中,以便继续遍历。
- 返回结果:遍历完成后,
result中存储了所有符合条件的路径,返回result作为最终结果。
关键点:
- DFS的迭代实现:通过栈来迭代实现深度优先搜索,而非递归,有效地遍历了二叉树的每个节点。
- 路径和的动态更新:在遍历过程中,动态计算和更新每条路径上的节点值之和,确保只有当路径和等于目标和时,路径才会被添加到结果集中。
- 路径的回溯:通过在每次迭代中创建新的路径列表(基于当前路径的深拷贝并添加新节点),算法模拟了路径的探索与回溯过程。这确保了每个节点在路径中的正确位置,并允许在遍历到叶子节点时回溯。
代码展示
java
public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
List<List<Integer>> result = new ArrayList<>();
if (root == null) {
return result;
}
// 使用三个栈来分别存储节点、到当前节点的路径和、以及构成这个路径和的节点列表
Deque<TreeNode> nodeStack = new LinkedList<>();
Deque<Integer> pathSumStack = new LinkedList<>();
Deque<List<Integer>> pathStack = new LinkedList<>();
// 将根节点及其相关信息加入栈中
nodeStack.push(root);
pathSumStack.push(root.val);
List<Integer> path = new ArrayList<>();
path.add(root.val);
pathStack.push(path);
while (!nodeStack.isEmpty()) {
TreeNode currentNode = nodeStack.pop();
int currentPathSum = pathSumStack.pop();
List<Integer> currentPath = pathStack.pop();
// 当前节点是叶子节点,并且路径和等于目标值
if (currentNode.left == null && currentNode.right == null && currentPathSum == targetSum) {
// 深拷贝,规避Java的引用传递的特性
List<Integer> temp = new ArrayList<>(currentPath);
result.add(temp);
}
// 遍历子节点
if (currentNode.right != null) {
// 将子节点及其路径和、路径列表推入各自的栈
nodeStack.push(currentNode.right);
pathSumStack.push(currentPathSum + currentNode.right.val);
List<Integer> newPath = new ArrayList<>(currentPath);
newPath.add(currentNode.right.val);
pathStack.push(newPath);
}
if (currentNode.left != null) {
nodeStack.push(currentNode.left);
pathSumStack.push(currentPathSum + currentNode.left.val);
List<Integer> newPath = new ArrayList<>(currentPath);
newPath.add(currentNode.left.val);
pathStack.push(newPath);
}
}
// 返回找到的所有路径
return result;
}时间复杂度:O(n * logn),其中N是树中节点的数量。每个节点都被访问一次(O(n)),并且对于每个节点,路径列表可能被复制(深拷贝),复制的时间复杂度最坏为O(logn),即树的高度。
空间复杂度:O(n * logn),主要空间开销来源于存储结果的列表和栈。最坏情况下,存储所有路径需要的空间和栈的空间复杂度都与树的大小和形状有关。
总结
如果可以将大问题转化为一个小问题,那就可以考虑使用递归方法了。
