59.螺旋矩阵Ⅱ
难度:中等
给你一个正整数 n ,生成一个包含 1 到 n^(2) 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
示例 1:
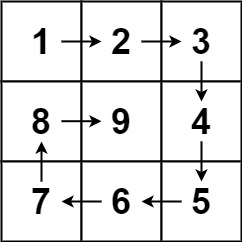
输入:n = 3
输出:[[1,2,3],[8,9,4],[7,6,5]]示例 2:
输入:n = 1
输出:[[1]]提示:
1 <= n <= 20
解题思路
很容易想到的一种做法是暴力模拟:
- 初始化二维矩阵,全部填充为0
- 按照 右、下、左、上的方向对矩阵从外向内进行填充
- 每当遇到矩阵边界的时候,就改变填充方向
- 所有数据全部填充完毕的时候,矩阵就完成了
我的代码
java
class Coordinate {
int start;
int x;
int y;
public Coordinate(int start, int x, int y) {
this.start = start;
this.x = x;
this.y = y;
}
}
public int[][] generateMatrix(int n) {
int[][] result = new int[n][n];
result[0][0] = 1;
Coordinate coordinate = new Coordinate(1, 0, 0);
while (coordinate.start < n * n) {
toBorder(result, coordinate, n, "右");
toBorder(result, coordinate, n, "下");
toBorder(result, coordinate, n, "左");
toBorder(result, coordinate, n, "上");
}
return result;
}
public void toBorder(int[][] result, Coordinate coordinate, int n, String direction) {
int start = coordinate.start;
int x = coordinate.x;
int y = coordinate.y;
if ("上".equals(direction)) {
int i;
for (i = 0; i < n - 1 && result[x - 1 - i][y] == 0; i++) {
result[x - 1 - i][y] = start + 1 + i;
}
coordinate.x = x - i;
coordinate.y = y;
coordinate.start = coordinate.start + i;
} else if ("下".equals(direction)) {
int i;
for (i = 0; i < n - 1 && result[x + 1 + i][y] == 0; i++) {
result[x + 1 + i][y] = start + 1 + i;
}
coordinate.x = x + i;
coordinate.y = y;
coordinate.start = coordinate.start + i;
} else if ("左".equals(direction)) {
int i;
for (i = 0; i < n - 1 && result[x][y - 1 - i] == 0; i++) {
result[x][y - 1 - i] = start + 1 + i;
}
coordinate.x = x;
coordinate.y = y - i;
coordinate.start = coordinate.start + i;
} else if ("右".equals(direction)) {
int i;
for (i = 0; i < n - 1 && result[x][y + 1 + i] == 0; i++) {
result[x][y + 1 + i] = start + 1 + i;
}
coordinate.x = x;
coordinate.y = y + i;
coordinate.start = coordinate.start + i;
}
}时间复杂度:O(n^(2))
空间复杂度:O(n^(2))
更简洁写法
思路:
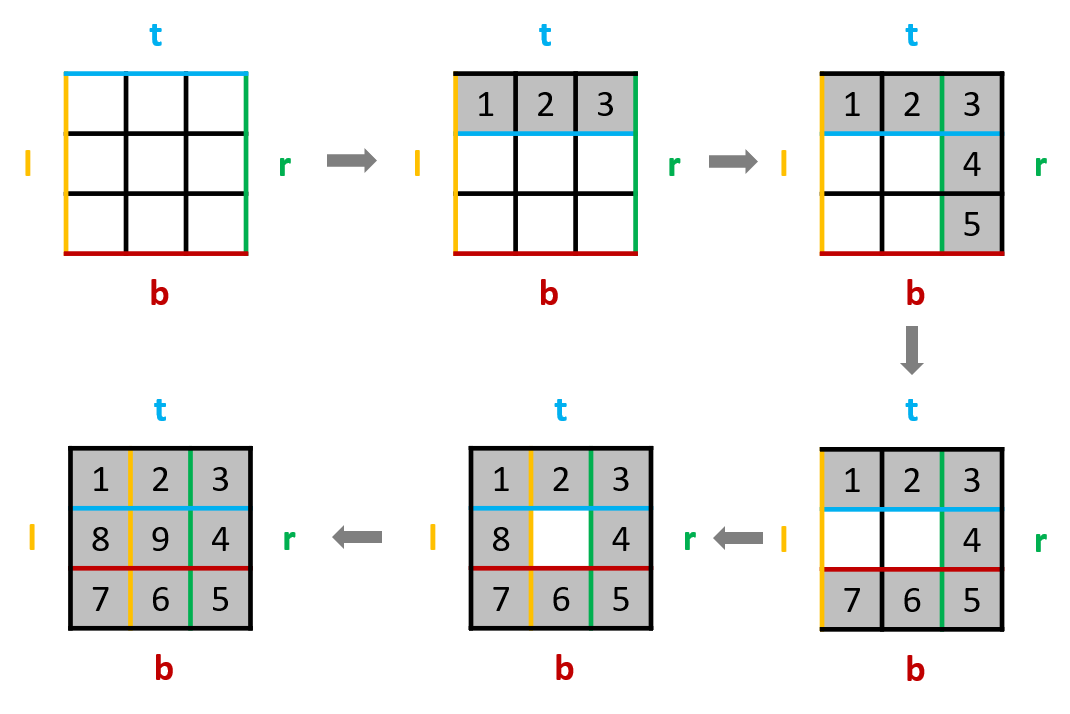
生成一个 n×n 空矩阵 result,随后模拟整个向内环绕的填入过程:
定义当前左右上下边界 left、right、top、bottom,初始值 num = 1,迭代循环条件为 num <= n * n 或者
当 num <= n * n 时,始终按照 从左到右、从上到下、从右到左、从下到上 的填入顺序循环,每次填入时:
执行 num ++:得到下一个需要填入的数字
更新边界:例如从左到右填完后,上边界 top++,相当于上边界向内缩 1 格
使用 num <= n * n 而不是 left < right || top < bottom 作为迭代条件,是为了解决当 n 为奇数时,矩阵中心数字无法在迭代过程中被填充的问题。
最终返回 result 即可
java
public int[][] generateMatrix(int n) {
int left = 0, right = n - 1, top = 0, bottom = n - 1;
int[][] result = new int[n][n];
int num = 1;
while (start <= n * n) {
for (int i = left; i <= right; i++) {
result[top][i] = num++;
}
top++;
for (int i = top; i <= bottom; i++) {
result[i][right] = num++;
}
right--;
for (int i = right; i >= left; i--) {
result[bottom][i] = num++;
}
bottom--;
for (int i = bottom; i >= top; i--) {
result[i][left] = num++;
}
left++;
}
return result;
}总结
本题并不涉及到什么算法,就是模拟过程,但却十分考察对代码的掌控能力。
模拟顺时针画矩阵的过程:
- 填充上行从左到右
- 填充右列从上到下
- 填充下行从右到左
- 填充左列从下到上
由外向内一圈一圈这么画下去。
可以发现这里的边界条件非常多,需要坚持 循环不变量 的规则才好得到答案。
