106.从中序和后序遍历序列构造二叉树
难度:中等
给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。
示例 1:
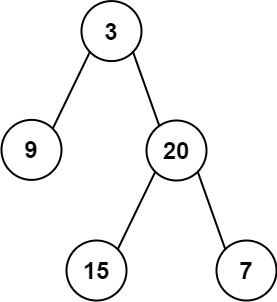
输入:inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出:[3,9,20,null,null,15,7]示例 2:
输入:inorder = [-1], postorder = [-1]
输出:[-1]提示:
1 <= inorder.length <= 3000postorder.length == inorder.length-3000 <= inorder[i], postorder[i] <= 3000inorder和postorder都由 不同 的值组成postorder中每一个值都在inorder中inorder保证是树的中序遍历postorder保证是树的后序遍历
解题思路
根据两种遍历序列,可以确定一棵二叉树。
这里需要注意的是,两个序列中必须有一个中序序列才可以。 前序和后序组合无法确定一棵二叉树。
根据三种遍历方式的特性,可以知道:**后序遍历中最后一个节点是树的根节点。而在中序序列中找到此节点可知:该节点左边则是根节点的左子树,右边是右子树。 **
我们基于此理论,就可以很轻松想出本题的解题思路,但是本题的难点在于边界条件的把握。
思路概括:
- 获取后序遍历序列的最后一个元素 A,就是当前的中间节点
- 从中序遍历序列中找到 A 元素,并将中序遍历序列从这里切割为 中序左序列 B 和 中序右序列 C,B 中可以获取到元素 A 的左子树,C 中可以获取到元素 A 的右子树
- 从后序遍历序列中从前往后,获取长度和 B 相同的序列 D,再获取长度和 C 相同的序列 E
- B 和 D 配对,C 和 E 配对,递归处理。
代码步骤:
- 基本情况:如果当前中序遍历的范围无效(
inorderEnd < inorderBegin),则说明子树为空,返回null。 - 根节点确定:后序遍历的最后一个元素总是当前子树的根节点。该函数首先创建根节点。
- 寻找根节点在中序遍历中的位置:通过线性搜索中序遍历数组来找到根节点的值,确定左右子树的范围。这一步是确定左右子树的关键。
- 计算左子树的大小:左子树的大小等于根节点在中序遍历中的位置减去中序遍历开始位置的差值。
- 构建左子树:递归地调用
build函数,使用中序遍历和后序遍历的左子树范围,构建左子树。 - 构建右子树:同样,递归地调用
build函数,使用中序遍历和后序遍历的右子树范围,构建右子树。
代码展示
java
public TreeNode buildTree(int[]inorder,int[]postorder){
TreeNode root=build(inorder,0,inorder.length-1,postorder,0,postorder.length-1);
return root;
}
public TreeNode build(int[]inorder,int inorderBegin,int inorderEnd,int[]postorder,int postorderBegin,int postorderEnd){
// 当前树为空
if(inorderEnd<inorderBegin){
return null;
}
// 根节点总是后序遍历的最后一个元素
int rootValue=postorder[postorderEnd];
// 创建根节点
TreeNode root=new TreeNode(rootValue);
// 在中序遍历中找到根节点的位置,确定左右子树的范围
int rootIndexInOrder=inorderBegin;
while(inorder[rootIndexInOrder]!=rootValue){
rootIndexInOrder++;
}
// 计算左子树的大小
int leftTreeSize=rootIndexInOrder-inorderBegin;
// 递归构建左子树和右子树
// 左子树的后序遍历结束位置可以通过左子树大小加上后序遍历的开始位置计算得到
root.left=build(inorder,inorderBegin,rootIndexInOrder-1,postorder,postorderBegin,postorderBegin+leftTreeSize-1);
// 右子树的后序遍历开始位置同理
root.right=build(inorder,rootIndexInOrder+1,inorderEnd,postorder,postorderBegin+leftTreeSize,postorderEnd-1);
return root;
}时间复杂度:O(n^2),最坏情况下,对于每个节点,都需要在中序遍历数组中进行一次线性搜索来找到根节点,这导致了 O(n) 的搜索时间复杂度。由于这个搜索过程对于树中的每个节点都要执行一次,总的时间复杂度为 O(n^2)。
空间复杂度:O(n) ,主要消耗在递归调用栈上。在最坏的情况下,这个栈的深度与树的高度相同。对于平衡二叉树,高度大约为logn,因此空间复杂度为O(logn)。
总结
递归的边界条件需要细心处理。
为了优化时间复杂度,可以先将中序遍历的数组值和索引映射关系存储在一个哈希表中,这样在查找根节点在中序遍历中的位置时,可以将时间复杂度从 O(n) 降低到 O(1)。这样总的时间复杂度就可以降低到 O(n),其中 N 是树中的节点数。
