112.路径总和
难度:中等
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。
叶子节点 是指没有子节点的节点。
示例 1:
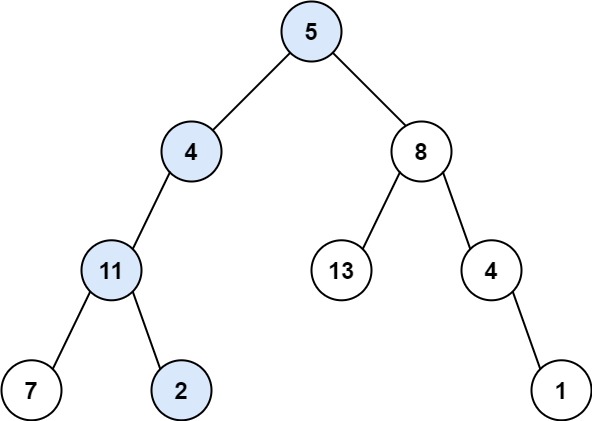
输入:root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出:true
解释:等于目标和的根节点到叶节点路径如上图所示。示例 2:
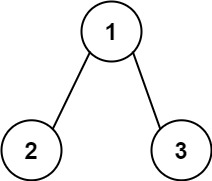
输入:root = [1,2,3], targetSum = 5
输出:false
解释:树中存在两条根节点到叶子节点的路径:
(1 --> 2): 和为 3
(1 --> 3): 和为 4
不存在 sum = 5 的根节点到叶子节点的路径。示例 3:
输入:root = [], targetSum = 0
输出:false
解释:由于树是空的,所以不存在根节点到叶子节点的路径。提示:
- 树中节点的数目在范围
[0, 5000]内 -1000 <= Node.val <= 1000-1000 <= targetSum <= 1000
递归法
观察要求我们完成的函数,我们可以归纳出它的功能:查找是否存在从当前节点 root 到叶子节点的路径,满足其路径和为 sum。
假定从根节点到当前节点的值之和为 sum_t,我们可以 将这个大问题转化为一个小问题 :是否存在从当前节点的子节点到叶子的路径,满足其路径和为 sum - sum_t。
不难发现这满足递归的性质:
- 若当前节点就是叶子节点,那么我们直接判断
sum是否等于val即可(因为路径和已经确定,就是当前节点的值,我们只需要判断该路径和是否满足条件)。 - 若当前节点不是叶子节点,我们只需要递归地询问它的子节点是否能满足条件即可。
代码展示
java
public boolean hasPathSum(TreeNode root,int targetSum){
if(root==null){
return false;
}
if(root.left==null&&root.right==null&&root.val==targetSum){
return true;
}
return hasPathSum(root.left,targetSum-root.val)||hasPathSum(root.right,targetSum-root.val);
}时间复杂度:O(n),其中 n 是二叉树的节点数。每一个节点恰好被遍历一次。
空间复杂度:O(h),其中 h 是树的高度。空间复杂度主要取决于递归时栈空间的开销,最坏情况下,树呈现链状,空间复杂度为 O(n) 。平均情况下树的高度与节点数的对数正相关,空间复杂度为 O(logn)。
前序遍历+栈+回溯法
联想 257.二叉树的所有路径 题,我们可以想到使用前序遍历的方式,记录从根节点到当前节点的路径和。
这样我们使用两个栈:一个用于存储节点(nodeStack),另一个用于存储到当前节点为止的路径和(pathSumStack)
算法步骤:
- 初始条件检查:如果根节点
root为空,则直接返回false,表示没有路径可以满足条件。 - 初始化栈:创建两个栈,
nodeStack用于存储遍历过程中的节点,pathSumStack用于存储到当前节点为止的路径和。根节点及其值被推入各自的栈作为初始值。 - 迭代遍历:使用一个循环,当
nodeStack不为空时进行迭代。每次迭代中,从栈中弹出一个节点(currentNode)和对应的路径和(currentPathSum)。- 叶子节点检查:如果当前节点是叶子节点(即没有左右子节点),并且其路径和等于
targetSum,则找到了满足条件的路径,返回true。 - 右子节点处理:如果当前节点有右子节点,将右子节点及其对应的路径和(当前路径和加上右子节点的值)推入各自的栈。这样做是为了保持深度优先的遍历顺序,由于栈是后进先出(LIFO)的数据结构,先处理的节点后弹出。
- 左子节点处理:同理,如果当前节点有左子节点,也将左子节点及其对应的路径和推入栈中。
- 叶子节点检查:如果当前节点是叶子节点(即没有左右子节点),并且其路径和等于
- 如果遍历完整棵树都没有找到满足条件的路径,则返回
false。
关键点:
- 深度优先搜索(DFS):通过栈实现非递归的深度优先搜索,以此来遍历树中的所有可能路径。
- 路径和的累计:对于每个节点,算法都计算了从根节点到该节点的路径和,并使用
pathSumStack来跟踪这个值。 - 叶子节点的特殊处理:只有当遍历到叶子节点时,算法才检查路径和是否等于
targetSum。
代码展示
java
public boolean hasPathSum(TreeNode root,int targetSum){
if(root==null){
return false;
}
Deque<TreeNode> nodeStack=new LinkedList<>();
Deque<Integer> pathSumStack=new LinkedList<>();
nodeStack.push(root);
pathSumStack.push(root.val);
while(!nodeStack.isEmpty()){
TreeNode currentNode=nodeStack.pop();
int currentPathSum=pathSumStack.pop();
// 如果是叶子节点,并且找到了目标路径
if(currentNode.left==null&¤tNode.right==null&¤tPathSum==targetSum){
return true;
}
// 因为栈是后进先出,所以先压入右孩子
if(currentNode.right!=null){
nodeStack.push(currentNode.right);
pathSumStack.push(currentPathSum+currentNode.right.val);
}
// 后压入左孩子
if(currentNode.left!=null){
nodeStack.push(currentNode.left);
pathSumStack.push(currentPathSum+currentNode.left.val);
}
}
return false;
}时间复杂度:O(n),其中n是树中节点的数量。算法访问每个节点恰好一次。
空间复杂度:O(h),其中h是树的高度。在最坏的情况下(树完全不平衡),空间复杂度可以退化到O(n)。空间复杂度主要由栈的使用决定,栈的最大深度等于树的高度。
总结
如果可以将大问题转化为一个小问题,那就可以考虑使用递归方法了。
