222.完全二叉树的节点个数
难度:容易
给你一棵 完全二叉树 的根节点 root ,求出该树的节点个数。
完全二叉树 的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层,则该层包含 1~ 2h 个节点。
示例 1:
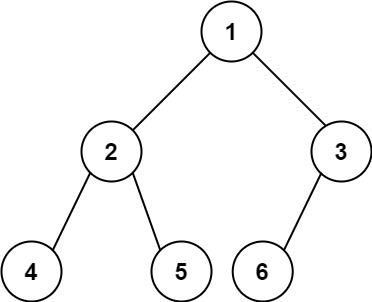
输入:root = [1,2,3,4,5,6]
输出:6示例 2:
输入:root = []
输出:0示例 3:
输入:root = [1]
输出:1提示:
- 树中节点的数目范围是
[0, 5 * 10^4] 0 <= Node.val <= 5 * 10^4- 题目数据保证输入的 树是 完全二叉树
**进阶:**遍历树来统计节点是一种时间复杂度为 O(n) 的简单解决方案。你可以设计一个更快的算法吗?
普通二叉树的递归法
采用递归的方式来解决问题,基于一个非常直观的原理:二叉树中的节点总数等于左子树中的节点数加上右子树中的节点数,再加上根节点自身。
算法步骤:
- 递归基准情况:如果当前节点为
null,说明这是一棵空树,因此返回节点数为0。 - 递归逻辑:如果当前节点不为空,算法会递归地计算左子树中的节点数和右子树中的节点数。然后,将这两个数相加,并加上
1(代表当前节点),从而得到包括当前节点在内的总节点数。 - 返回值:返回计算得到的节点总数。
代码展示
public int countNodes(TreeNode root) {
if (root == null) {
return 0;
}
return countNodes(root.left) + countNodes(root.right) + 1;
}时间复杂度:O(n),其中 n 是二叉树的节点数。每一个节点恰好被遍历一次。
空间复杂度:O(log n),算法的空间复杂度主要由递归调用栈的深度决定。在最坏情况下(二叉树完全不平衡,形成链状),空间复杂度为O(n)。在最好情况下(二叉树完全平衡),空间复杂度为O(log n),因为树的高度为log n。
普通二叉树的迭代法
前中后序的遍历方法或者层序遍历都可以,加一个统计节点个数的变量即可。
这里我采用层序遍历:
队列具有 先进先出 的特性,符合层序遍历的逻辑。这种层序遍历的方式就是图论中的广度优先遍历,只不过我们应用在了二叉树上。
算法流程:
处理特例:若根节点为空,则返回 0
初始化节点个数 result 为0,根节点入队
BFS 循环: 判断队列是否为空。如果不为空,说明还有节点需要遍历
初始化当前层的节点个数
currentLevelSize为队列的大小。使用一个内层循环,遍历当前层的节点。循环次数为当前层的节点个数
currentLevelSize。- 从队列中取出一个节点
current,result值增加 - 如果当前节点有左子节点,将左子节点入队。
- 如果当前节点有右子节点,将右子节点入队。
- 从队列中取出一个节点
此时队列中已经把当前层的节点都出队了,同时把下一层的节点都入队了,因此队列大小刚好变成了下一层的节点个数。
返回结果 result
代码展示
public int countNodes(TreeNode root) {
// 若根节点为空,则返回0
if (root == null) {
return 0;
}
int result = 0;
Deque<TreeNode> queue = new LinkedList<>();
// 根节点入队
queue.add(root);
// BFS 循环
while (!queue.isEmpty()) {
int currentLayerSize = queue.size();
// 这里一定要使用固定大小currentLayerSize,不要使用queue.size(),因为queue不停地出队入队,所以其大小是不断变化的
for (int i = 0; i < currentLayerSize; i++) {
TreeNode current = queue.poll();
result++;
if (current.left != null) {
queue.add(current.left);
}
if (current.right != null) {
queue.add(current.right);
}
}
}
return result;
}时间复杂度:O(n),其中 n 是二叉树的节点数。每一个节点恰好被遍历一次。
空间复杂度:O(n),最差情况下,即当树为满二叉树时,最多有 (n+1)/2 个树节点 同时 在 queue 中,故使用 O(n) 大小的额外空间。
完全二叉树的递归法
在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。
若最底层为第 h 层,则该层的节点个数范围为 1~ 2^(h-1) 。
完全二叉树的形态只有两种情况:
- 满二叉树
- 最后一层叶子节点没有满
对于情况一,节点总数可以直接用 2^h - 1 来计算,注意这里根节点深度为 1。
对于情况二,节点总数的计算,可以通过分别递归左孩子,和右孩子,递归到某一深度一定会有左孩子或者右孩子为满二叉树,然后依然可以按照情况 1 来计算。
那么这里有两个问题:
- 如何快速获知一棵 完全二叉树 是不是满二叉树
- 如何快速获得一颗 完全二叉树 的层数
一个定理:在完全二叉树中,从根节点出发,如果向左遍历的深度等于向右遍历的深度,说明该完全二叉树就是满二叉树。
基于这个定理,我们一下子就可以同时解决上述两个问题。
算法步骤:
- 初始检查:如果根节点
root为空,则该树没有节点,返回0。 - 计算深度:分别计算左子树和右子树的深度。这里的深度计算是通过连续访问左子树的左孩子和右子树的右孩子直到叶子节点来完成的,分别得到左深度
leftDepth和右深度rightDepth。 - 检查是否为满二叉树:
- 如果左深度等于右深度,说明这是一个满二叉树。对于满二叉树,节点总数可以直接通过公式
2^(深度 + 1) - 1计算得到,其中深度是从0开始的。 - 这里深度加
1的原因是算法中计算的深度实际上是从根节点到最左/最右叶子节点的路径长度,而在公式中需要的是整棵树的层数。
- 如果左深度等于右深度,说明这是一个满二叉树。对于满二叉树,节点总数可以直接通过公式
- 递归计算:如果树不是满二叉树,那么就递归地计算左子树和右子树的节点数,并加上根节点自身(
+1)。
代码展示
public int countNodes(TreeNode root) {
// 若根节点为空,则返回0
if (root == null) {
return 0;
}
TreeNode left = root.left;
TreeNode right = root.right;
int leftDepth = 0, rightDepth = 0;
while (left != null) { // 求左子树深度
left = left.left;
leftDepth++;
}
while (right != null) { // 求右子树深度
right = right.right;
rightDepth++;
}
// 根据左深度和右深度是否相同来判断该子树是不是满二叉树
if (leftDepth == rightDepth) {
return (int) (Math.pow(2, leftDepth + 1) - 1);
}
return countNodes(root.left) + countNodes(root.right) + 1;
}时间复杂度:O(logn * logn),这是因为每次递归调用都会减少树的高度,而计算树的高度本身需要 O(logn) 的时间。
空间复杂度:O(log n),算法的空间复杂度主要由递归调用栈的深度决定。在最坏情况下(二叉树完全不平衡,形成链状),空间复杂度为O(n)。在最好情况下(二叉树完全平衡),空间复杂度为O(log n),因为树的高度为log n。
总结
在完全二叉树中,从根节点出发,如果向左遍历的深度等于向右遍历的深度,说明该完全二叉树就是满二叉树
