226.翻转二叉树
难度:容易
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
示例 1:
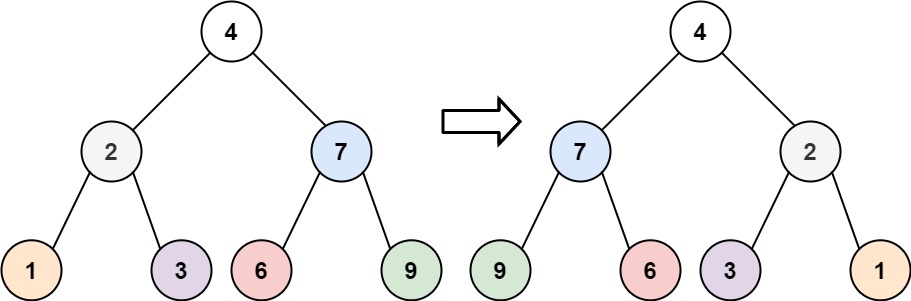
输入:root = [4,2,7,1,3,6,9]
输出:[4,7,2,9,6,3,1]示例 2:
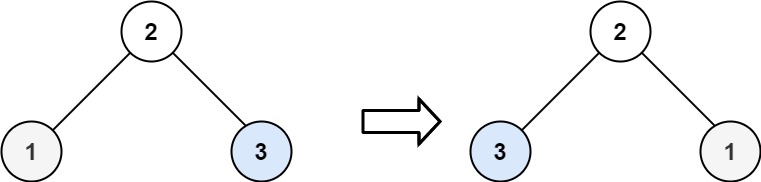
输入:root = [2,1,3]
输出:[2,3,1]示例 3:
输入:root = []
输出:[]提示:
- 树中节点数目范围在
[0, 100]内 -100 <= Node.val <= 100
层序遍历+队列法
参考 102 题,使用层序遍历的方法,将每个节点的左右孩子进行翻转即可。
层序遍历一个二叉树。就是从左到右、一层一层地去遍历二叉树。这种遍历的方式需要借用一个辅助数据结构即队列来实现。
队列具有 先进先出 的特性,符合层序遍历的逻辑。这种层序遍历的方式就是图论中的广度优先遍历,只不过我们应用在了二叉树上。
算法流程:
- 处理特例:若根节点为空,则返回空
- 根节点入队
- BFS 循环: 判断队列是否为空。如果不为空,说明还有节点需要遍历
- 初始化当前层的节点个数
currentLevelSize为队列的大小。 - 使用一个内层循环,遍历当前层的节点。循环次数为当前层的节点个数
currentLevelSize。- 交换当前节点的左右子节点。
- 如果当前节点有左子节点,将左子节点入队。
- 如果当前节点有右子节点,将右子节点入队。
- 此时队列中已经把当前层的节点都出队了,同时把下一层的节点都入队了,因此队列大小刚好变成了下一层的节点个数。
- 初始化当前层的节点个数
- 返回翻转后的根节点
代码展示
java
public List<List<Integer>> levelOrder(TreeNode root) {
// 若根节点为空,则返回空列表
if (root == null) {
return null;
}
Deque<TreeNode> queue = new LinkedList<>();
// 根节点入队
queue.add(root);
// BFS 循环
while (!queue.isEmpty()) {
int currentLayerSize = queue.size();
// 这里一定要使用固定大小currentLayerSize,不要使用queue.size(),因为queue不停地出队入队,所以其大小是不断变化的
for (int i = 0; i < currentLayerSize; i++) {
TreeNode current = queue.poll();
// 交换左右子节点
TreeNode temp = current.left;
current.left = current.right;
current.right = temp;
if (current.left != null) {
queue.add(current.left);
}
if (current.right != null) {
queue.add(current.right);
}
}
result.add(currentLayerList);
}
return root;
}时间复杂度:O(n),其中 n 是二叉树的节点数。每一个节点恰好被遍历一次。
空间复杂度:O(n),最差情况下,即当树为满二叉树时,最多有 (n+1)/2 个树节点 同时 在 queue 中,故使用 O(n) 大小的额外空间。
前、后序遍历+递归法
递归法的基本思想是从根节点开始,递归地交换每个节点的左右子树。
对于每个节点,我们先交换其左右子节点,然后对其左子节点和右子节点分别递归执行相同的操作。
前、后序遍历都可以。中序不行,因为先左孩子交换孩子,再根节点交换孩子(做完后,右孩子已经变成了原来的左孩子),再右孩子交换孩子(此时其实是对原来的左孩子做交换)。
代码展示
java
public TreeNode invertTree(TreeNode root) {
// 如果当前节点为空,直接返回null
if (root == null) {
return null;
}
// 先交换当前节点的左右子节点
TreeNode temp = root.left;
root.left = root.right;
root.right = temp;
// 递归地对左右子树进行同样的操作
invertTree(root.left);
invertTree(root.right);
// 返回翻转后的根节点
return root;
}时间复杂度:O(n),其中 n 是二叉树的节点数。每一个节点恰好被遍历一次。
空间复杂度:O(1),因为这种做法没有使用队列,所以大大降低了空间复杂度。
总结
针对二叉树的问题,解题之前一定要想清楚究竟是前中后序遍历,还是层序遍历。
