239.滑动窗口最大值
难度:困难
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回 滑动窗口中的最大值 。
示例 1:
输入:nums = [1,3,-1,-3,5,3,6,7], k = 3
输出:[3,3,5,5,6,7]
解释:
滑动窗口的位置 最大值
--------------- -----
[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7示例 2:
输入:nums = [1], k = 1
输出:[1]提示:
1 <= nums.length <= 10^5-10^4 <= nums[i] <= 10^41 <= k <= nums.length
解题思路
暴力做法:每次滑动窗口的过程中,重新遍历窗口内的数据来找到最大的数值,这样很明显算法的时间复杂度为 O(k * n)。
本题难点在于, 如何在每次窗口滑动后,将 “获取窗口内最大值” 的时间复杂度从 O(k) 降低至 O(1) 。
在 155.最小栈 中,我们使用了 单调栈 来实现随意入栈、出栈情况下的 O(1) 时间获取 “栈内最小值” 。本题同理,不同点在于 “出栈操作” 删除的是 “列表尾部元素” ,而 “窗口滑动” 删除的是 “列表头部元素” 。
在滑动窗口形成及移动的过程中,我们注意到元素从窗口的右侧进入,多余的元素会从窗口的左侧移除。一端进入,另一端移除,这正是 队列 的性质,所以此题我们可以借助队列来求解。
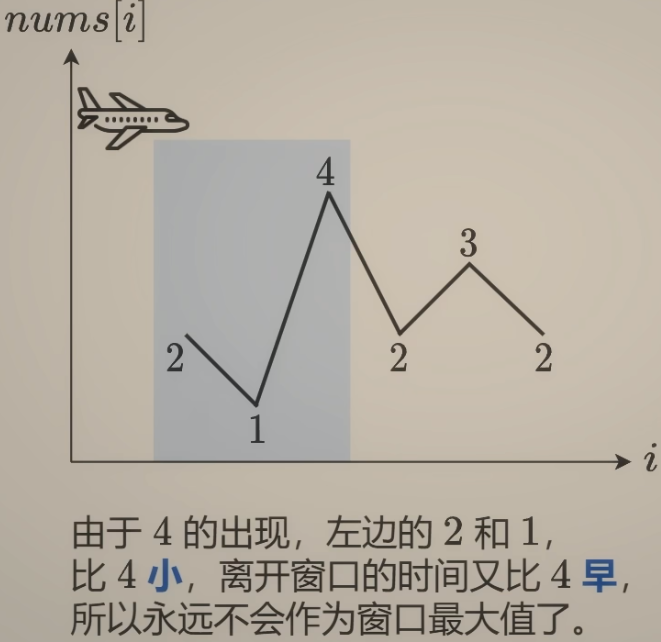
双端队列是一个可以从两端进行插入和删除操作的队列。在这个问题中,它被用来存储那些可能成为当前滑动窗口最大值的元素的索引(或者直接存储元素本身)。
代码流程:
- 创建一个双端队列
deque和一个数组result。deque用于存储当前滑动窗口中可能是最大值的元素,而result用于存储每个窗口的最大值。 - 遍历输入数组
nums。对于每个元素,执行以下操作:- 检查队列的头部元素(即最大值候选)是否还在滑动窗口内。如果不在(即它是窗口左侧即将移出的元素),则从队列头部移除。
- 从队列尾部开始,移除所有比当前元素小的元素。 因为这些元素不可能再成为窗口的最大值了(有一个更大的值进入了窗口),并且它们位于新元素之前,因此在未来的窗口中也不用再被考虑了。
- 将当前元素添加到双端队列的尾部。
- 当窗口的大小达到
k时,窗口的最大值就是队列头部的元素。将这个值添加到result数组中。
关键点:
- 双端队列头部始终是当前窗口的最大值:通过移除比当前元素小的元素,队列头部始终保持为当前窗口的最大值。且队列头部以后的元素,代表着如果首元素被移除窗口后,新窗口内的最大元素。
- 双端队列的更新与窗口的滑动同步进行:队列的更新发生在每次窗口滑动时,即每次迭代中。
我的代码
java
public int[] maxSlidingWindow(int[] nums, int k) {
int ln = nums.length;
Deque<Integer> deque = new LinkedList<>();// 存储元素的双端队列
int[] result = new int[ln - k + 1];// 存储结果
for (int i = 0; i < ln; i++) {
// 当窗口已经形成,开始滑动时,移除不再属于窗口的元素
if (i > k - 1 && deque.peekFirst() == nums[i - k]) {
deque.pollFirst();
}
// 从队列尾部往前搜索,移除所有比当前元素小的元素
while (!deque.isEmpty() && deque.peekLast() < nums[i]) {
deque.pollLast();
}
// 将当前元素添加到队列尾部
deque.addLast(nums[i]);
// 当当窗口大小达到 k 时,说明窗口已经完全形成,将队列头部的元素(最大值)添加到结果中
if (i >= k - 1) {
result[i - k + 1] = deque.peekFirst();
}
}
return result;
}时间复杂度:O(n)
空间复杂度:O(n)
可以将 未形成窗口 和 形成窗口后 两个阶段拆分到两个循环里实现。代码虽变长,但减少了冗余的判断操作,且思路会更加清晰:
java
public int[] maxSlidingWindow(int[] nums, int k) {
int ln = nums.length;
Deque<Integer> deque = new LinkedList<>();// 存储元素的双端队列
int[] result = new int[ln - k + 1];// 存储结果
// 还未形成窗口
for (int i = 0; i < k; i++) {
// 从队列尾部往前搜索,移除所有比当前元素小的元素
while (!deque.isEmpty() && deque.peekLast() < nums[i])
deque.pollLast();
deque.addLast(nums[i]);
}
// 当窗口大小达到 k 时,说明窗口已经完全形成,将队列头部的元素(最大值)添加到结果中
result[0] = deque.peekFirst();
for (int i = k; i < ln; i++) {
// 当窗口已经形成,开始滑动时,移除不再属于窗口的元素
if (deque.peekFirst() == nums[i - k]) {
deque.pollFirst();
}
// 从队列尾部往前搜索,移除所有比当前元素小的元素
while (!deque.isEmpty() && deque.peekLast() < nums[i]) {
deque.pollLast();
}
// 将当前元素添加到队列尾部
deque.addLast(nums[i]);
// 当窗口大小达到 k 时,说明窗口已经完全形成,将队列头部的元素(最大值)添加到结果中
result[i - k + 1] = deque.peekFirst();
}
return result;
}总结
双端队列:普通队列是只能在队尾进行插入,在队头进行删除操作的线性表。而双端队列则是放开了这个限制,在队头和队尾两端都可以进行入队和出队操作。
**单调队列:**队列里的元素都是按递增(递减)的顺序队列,这个队列的头是最小(最大)的元素。
