257.二叉树的所有路径
难度:容易
给你一个二叉树的根节点 root ,按 任意顺序 ,返回所有从根节点到叶子节点的路径。
叶子节点 是指没有子节点的节点。
示例 1:
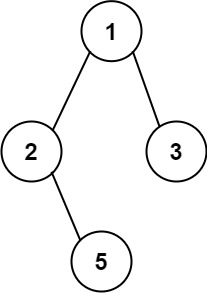
输入:root = [1,2,3,null,5]
输出:["1->2->5","1->3"]示例 2:
输入:root = [1]
输出:["1"]提示:
- 树中节点的数目在范围
[1, 100]内 -100 <= Node.val <= 100
前序遍历+递归+回溯法
这道题目要求从根节点到叶子的路径,所以需要前序遍历,这样才方便让父节点指向孩子节点,找到对应的路径。
二叉树的前序遍历代码如下:
java
public List<Integer> preorderTraversal(TreeNode root){
List<Integer> result=new ArrayList<>();
preorder(root,result);
return result;
}
public void preorder(TreeNode root,List<Integer> result){
if(root==null){
return;
}
result.add(root.val);
preorder(root.left,result);
preorder(root.right,result);
}我们完全可以仿照上面的代码来写。
算法步骤:
- 初始化结果列表:创建一个
List<String>来存储所有路径的字符串表示。 - 边界条件处理:如果根节点
root为空,即树为空,直接返回空的结果列表。 - 递归遍历树:使用
preorder方法递归地遍历树。为了记录当前的路径,方法接收一个StringBuilder对象path和结果列表result。
preorder方法:
- 基本情况:如果当前节点为空,即到达了叶子节点的子节点,直接返回。
- 路径记录:首先,记录当前
path的长度,这将用于之后恢复path的状态。如果当前path不为空(即当前节点不是根节点),则在path中追加"->"。然后,追加当前节点的值。 - 叶子节点检测:如果当前节点是叶子节点(即左右子节点都为空),则将当前的
path转换为字符串并添加到结果列表中。 - 递归子节点:如果当前节点不是叶子节点,递归调用
preorder方法遍历左子节点和右子节点。 - 路径状态恢复:在返回之前,将
path的长度还原到进入当前节点前的状态。这一步骤确保了每次递归返回时,path都只包含从根节点到当前节点的路径。
关键点:
- 路径的动态构建和回溯:通过
StringBuilder来动态构建路径,在每次递归调用后通过setLength方法回溯,确保路径状态正确。这样避免了创建大量的字符串或列表对象,提高了效率。 - 使用前序遍历:该算法通过前序遍历(根-左-右)的方式访问树中的每个节点,确保路径按照从根到叶子的顺序被构建。
- 递归与回溯:算法的精髓在于递归遍历和适时回溯,以正确构建并记录每一条从根到叶子的路径。
代码展示
java
public List<String> binaryTreePaths(TreeNode root){
List<String> result=new ArrayList<>();
if(root==null){
return result;
}
StringBuilder path=new StringBuilder();
preorder(root,path,result);
return result;
}
public void preorder(TreeNode root,StringBuilder path,List<String> result){
if(root==null){
return;
}
int length=path.length(); // 记录进入这个节点前路径的长度
if(length>0){ // 不是根节点,需要加上"->"
path.append("->");
}
path.append(root.val);
if(root.left==null&&root.right==null){ // 叶子节点,添加路径到结果列表
result.add(path.toString());
}else{ // 非叶子节点,递归遍历
preorder(root.left,path,result);
preorder(root.right,path,result);
}
path.setLength(length); // 恢复路径到进入这个节点前的状态
}时间复杂度:O(n)
空间复杂度:O(n)
前序遍历+迭代+回溯法
可以使用前序遍历的迭代方式来模拟遍历路径的过程:
- 初始化栈:使用两个栈,一个用于存储节点(
nodeStack),另一个用于存储到达每个节点的路径(pathStack)。初始时,根节点及其值作为路径被推入各自的栈。 - 迭代遍历:在迭代过程中,每次从栈中弹出一个节点和对应的路径。如果该节点是叶子节点,将当前路径添加到结果列表中。
- 子节点处理:对于每个非叶子节点,检查其左右子节点。如果存在子节点,则将这些子节点及其对应的路径(当前路径加上"->" 和子节点的值)推入栈中,以便后续处理。
- 结果返回:遍历结束后,所有从根到叶的路径都被收集到结果列表中,函数返回这个列表。
代码展示
java
public List<String> binaryTreePaths(TreeNode root){
List<String> result=new ArrayList<>();
if(root==null){
return result;
}
Deque<TreeNode> nodeStack=new LinkedList<>();
Deque<String> pathStack=new LinkedList<>();
nodeStack.push(root);
pathStack.push(Integer.toString(root.val));
while(!nodeStack.isEmpty()){
TreeNode currentNode=nodeStack.pop();
String currentPath=pathStack.pop();
// 如果是叶子节点,添加当前路径到结果列表
if(currentNode.left==null&¤tNode.right==null){
result.add(currentPath);
}
// 因为栈是后进先出,所以先压入右孩子
if(currentNode.right!=null){
nodeStack.push(currentNode.right);
pathStack.push(currentPath+"->"+currentNode.right.val);
}
// 后压入左孩子
if(currentNode.left!=null){
nodeStack.push(currentNode.left);
pathStack.push(currentPath+"->"+currentNode.left.val);
}
}
return result;
}时间复杂度:O(n),其中N是树中节点的数量。算法访问了树的每个节点恰好一次。
空间复杂度:O(n) ,最坏情况下(例如完全不平衡的树),栈的大小可能与树的节点数相等。对于路径的存储,最坏情况下(假设树完全展开)路径字符串的总长度也是O( n)。
总结
回溯和递归是一一对应的,有一个递归,就要有一个回溯
