347.前k个高频元素
难度:中等
给你一个整数数组 nums 和一个整数 k ,请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。
示例 1:
输入: nums = [1,1,1,2,2,3], k = 2
输出: [1,2]示例 2:
输入: nums = [1], k = 1
输出: [1]提示:
1 <= nums.length <= 10^5k的取值范围是[1, 数组中不相同的元素的个数]- 题目数据保证答案唯一,换句话说,数组中前
k个高频元素的集合是唯一的
**进阶:**你所设计算法的时间复杂度 必须 优于 O(nlogn),其中 n 是数组大小。
暴力排序法
解题思路
暴力做法是使用 HashMap 来遍历一遍数组,得到每个元素和对应的出现频率,再根据 HashMap 的 value 值来进行降序排序,返回排序后前 k 个键值对的 key 即可。
代码展示
public int[] topKFrequent(int[] nums, int k) {
int ln = nums.length;
int[] result = new int[k];
HashMap<Integer, Integer> map = new HashMap<>();
// 使用 HashMap 统计每个元素的频率
for (int i = 0; i < ln; i++) {
int x = nums[i];
map.put(x, map.getOrDefault(x, 0) + 1);
}
// 创建一个列表,存放 Map 的条目,然后根据频率进行降序排序
List<Map.Entry<Integer, Integer>> list = new ArrayList<>(map.entrySet());
// Comparator 接口用于定义对象之间的比较规则,其约定如下:
// 返回值为负数,则第一个参数排在前面
// 返回值为正数,则第一个参数排在后面
list.sort((a, b) -> b.getValue() - a.getValue());
// 获取前 k 个高频元素
for (int i = 0; i < k; i++) {
result[i] = list.get(i).getKey();
}
return result;
}时间复杂度:O(n logn),主要由排序步骤决定。
空间复杂度:O(n)
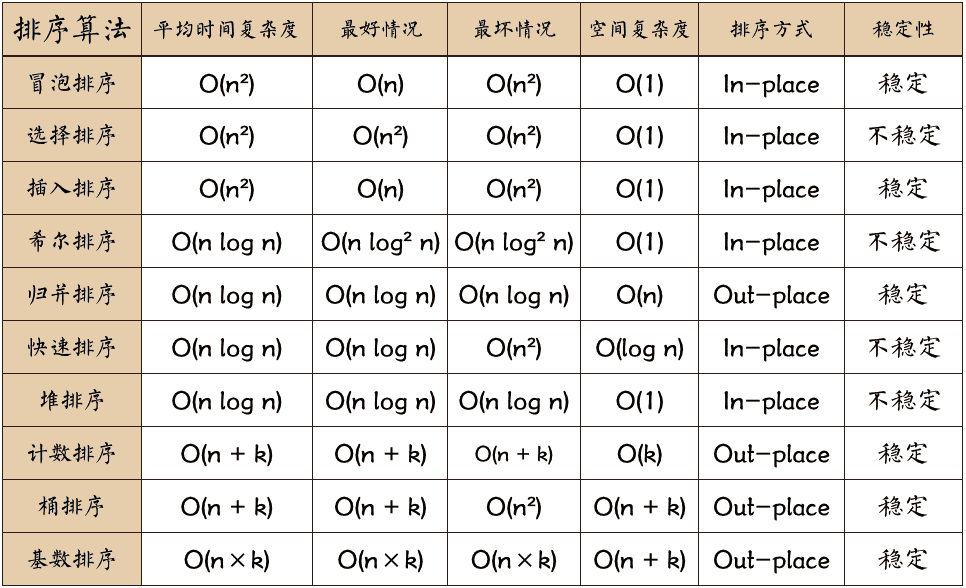
在不调用 list.sort() 的情况下,可以发现使用常规的排序算法,甚至快速排序都无法满足题目的要求,它们的时间复杂度都大于或者等于 O(nlogn),而题目要求算法的时间复杂度必须优于 O(n log n)。
堆(优先级队列)
堆是一种常用的树形结构,它是一种特殊的完全二叉树。
树中每个结点的值都不小于(或不大于)其左右孩子的值,这一特性称之为堆序性。
因此,在一个堆中,根节点是最大(或最小)节点。如果根节点最小,称之为小顶堆(或小根堆),如果根节点最大,称之为大顶堆(或大根堆)。
但堆的左右孩子没有大小的顺序。
堆的存储结构
堆一般都用数组来存储,i 节点的父节点下标就为 ( i – 1 ) / 2 。i 节点的左右子节点下标分别为 2 ∗ i + 1 和 2 ∗ i + 2。
堆的操作
- 建立:以最小堆为例,如果以数组存储元素时,一个数组具有对应的树表示形式,但树并不满足堆的条件,需要重新排列元素,可以建立“堆化”的树。
- 插入:每次插入都是将一个新元素插入到数组末尾,如果新构成的二叉树不满足堆的性质,我们需要将新元素 上浮 到数组末尾到堆顶的路径上(和父节点交换位置),直到找到属于自己的位置。
- 删除:删除一个元素总是发生在堆顶,因为堆顶的元素是最小的(小顶堆中)。数组中最后一个元素用来填补空缺位置,然后对顶部元素进行 下沉,如果左右孩子有比自己小的,则选择 最小 的那个进行交换。重复进行下沉操作,以满足堆的条件。
堆排序
堆排序的基本思想是:
- 将待排序的序列构造成一个大顶堆,根据大顶堆的性质,我们可知当前堆的根节点(堆顶)就是序列中最大的元素;
- 将堆顶元素和最后一个元素交换,然后将剩下的节点重新构造成一个大顶堆;
- 重复步骤2,如此反复,从第一次构建大顶堆开始,每一次构建,我们都能获得一个序列的最大值,然后把它放到大顶堆的尾部。最终我们将得到一个有序序列。
优先级队列
优先级队列,其实就是一个 披着队列外衣的堆,因为优先级队列的接口只有:从队头取元素 和 从队尾添加元素,所以看起来就是一个队列。
优先级队列的内部元素会依照元素的权值来自动排列。
解题思路
在这个问题中,我们使用小顶堆(最小堆)而不是大顶堆(最大堆)的原因是效率和实用性。我们的目标是找出数组中出现频率最高的 k 个元素。考虑以下几点:
- 堆的大小控制:当使用小顶堆时,堆的大小可以被限制为 k(大顶堆做这道题则需要对所有 n 个元素构建一个堆,随后执行 k 次删除操作来获取 k 个最高频元素)。这意味着,一旦堆的大小超过 k,我们可以删除堆顶的元素(即当前频率最低的元素)。通过这种方式,堆内只需要保持着当前频率最高的 k 个元素。
- 减少堆操作:在使用小顶堆时,你只需要对 n 个元素各执行一次堆操作(即添加操作,可能跟随一个删除操作)。而使用大顶堆则需要对所有 n 个元素构建一个堆,随后执行 k 次删除操作来获取 k 个最高频元素。当 n 很大而 k 较小时,小顶堆的方法会涉及更少的堆操作。
- 效率:在小顶堆中,每当一个新元素的频率高于堆顶元素的频率时,我们替换掉堆顶元素并重新调整堆。这个操作的时间复杂度是 O(log k)。相反,构建大顶堆的时间复杂度是 O(n log n)。因此,对于大数据集,小顶堆通常更有效率。
- 简化最终结果的获取:使用小顶堆在完成所有操作后,堆中剩下的就是频率最高的 k 个元素。我们只需将这些元素从堆中取出并放入结果数组即可。
总结起来,使用小顶堆可以更高效地控制堆的大小,并确保在整个过程中始终保留频率最高的 k 个元素。这样既减少了不必要的操作,也简化了从堆中获取最终结果的步骤。
综上所述,虽然大顶堆和小顶堆都可以解决这个问题,但是在大多数情况下,特别是当 k 相对于 n 较小时,使用小顶堆更为高效,因为它涉及的堆操作更少,且对内存的利用更优化。
代码展示
public int[] topKFrequent(int[] nums, int k) {
int ln = nums.length;
int[] result = new int[k];
HashMap<Integer, Integer> map = new HashMap<>();
// 使用 HashMap 统计每个元素的频率
for (int i = 0; i < ln; i++) {
int x = nums[i];
map.put(x, map.getOrDefault(x, 0) + 1);
}
// 创建一个最小堆,比较器根据元素频率来排序,频率较低的元素在堆顶
// 返回值为负数,则第一个参数排在前面
// 返回值为正数,则第一个参数排在后面
PriorityQueue<Integer> heap = new PriorityQueue<>((n1, n2) -> map.get(n1) - map.get(n2));
// 遍历 HashMap,将元素添加到堆中,同时维持堆的大小为 k
for (Map.Entry<Integer, Integer> entry : map.entrySet()) {
int num = entry.getKey();
heap.add(num);
// 如果堆的大小超过 k,删除堆顶元素(频率最低的元素)
if (heap.size() > k) {
heap.poll();
}
}
// 取出堆中的元素,构建结果数组
for (int i = k - 1; i >= 0; i--) {
result[i] = heap.poll();
}
return result;
}时间复杂度:O(n log k),其中 n 是数组 nums 的长度。每次堆操作(添加和删除)的时间复杂度为 O(log k),总共进行了 n 次操作。
空间复杂度:O(n + k),其中 O(n) 是用于存储频率的 HashMap,O(k) 是用于存储堆元素的空间。
桶排序(计数排序)
解题思路
使用桶排序解决这个问题是一个很好的选择,尤其是当你需要对大量数据进行排序时,它可以提供比传统比较排序更优的性能。
桶排序的基本思想是将元素分散到有限数量的桶中,然后分别对每个桶中的元素进行排序,最后合并这些桶中的元素。
对于频率排序的场景,我们可以将桶视为频率的集合,其中每个桶存储具有相同频率的元素。然后,我们可以从频率最高的桶开始,依次取出元素,直到达到所需的 k 个元素。
代码展示
public int[] topKFrequent(int[] nums, int k) {
int ln = nums.length;
int[] result = new int[k];
HashMap<Integer, Integer> map = new HashMap<>();
// 使用 HashMap 统计每个元素的频率
for (int i = 0; i < ln; i++) {
int x = nums[i];
map.put(x, map.getOrDefault(x, 0) + 1);
}
// 桶排序,创建一个列表数组,数组的长度为 nums 的长度 + 1
List<Integer>[] buckets = new ArrayList[ln + 1];
// 遍历 HashMap,使用频率作为桶的索引,将元素添加到相应的桶中
for (Map.Entry<Integer, Integer> entry : map.entrySet()) {
int num = entry.getKey();
int frequency = entry.getValue();
// 如果当前桶中还未建立对应的列表,此时就该初始化一个列表
if (buckets[frequency] == null) {
buckets[frequency] = new ArrayList<>();
}
buckets[frequency].add(num);
}
// 从后向前遍历桶,获取前 k 个高频元素
for (int i = ln; i >= 0 && k > 0; i--) {
if (buckets[i] != null) {
List<Integer> bucket = buckets[i];
for (int j = 0; k > 0 && j < bucket.size(); j++) {
result[--k] = bucket.get(j);
}
}
}
return result;
}时间复杂度:O(n),n 表示数组的长度。首先,遍历一遍数组统计元素的频率,这一系列操作的时间复杂度是 O(n);桶的数量为 n+1,所以桶排序的时间复杂度为 O(n);因此,总的时间复杂度是 O(n)。
空间复杂度:O(n)
在这个特定的桶排序实现中,数组的长度设置为 nums 数组的长度加一 (nums.length + 1) 的原因是为了确保数组可以容纳从 0 到 nums.length(含)所有可能的频率。
这是因为:
- 最小可能的频率是 1(每个元素至少出现一次)。
- 最大可能的频率是
nums.length,这种情况发生在所有元素都相同的时候,即这个元素出现了nums.length次。
因此,我们需要一个能够覆盖从 1 到 nums.length 的频率范围的数组,所以数组长度需要是 nums.length + 1。这样,数组的每个索引(从 1 到 nums.length)都对应于一个可能的频率。索引 0 不会被使用,因为不存在频率为 0 的元素(每个元素至少出现一次)。
这个桶排序方法利用了频率作为索引的事实,是一个针对特定情况(即元素频率排序)优化的实现。在这种情况下,它非常有效,因为它避免了比较排序算法的复杂性,能够更快地聚集和排序大量数据。
总结
牢记十大排序方法,非常重要。
