530.二叉搜索树的最小绝对差

难度：简单

给你一个二叉搜索树的根节点 root ，返回 树中任意两不同节点值之间的最小差值 。

差值是一个正数，其数值等于两值之差的绝对值。

示例 1：

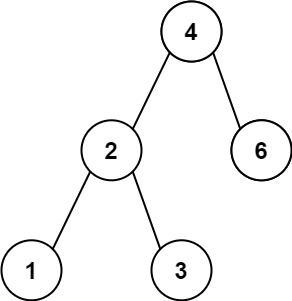
输入：root = [4,2,6,1,3]
输出：1

示例 2：

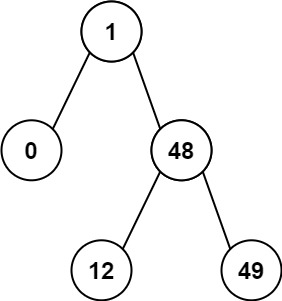
输入：root = [1,0,48,null,null,12,49]
输出：1

提示：

• 树中节点的数目范围是 [2, 104]
• 0 <= Node.val <= 105

解题思路

二叉搜索树的两大性质：

1. 二叉搜索树是一个有序树：
   • 若它的左子树不空，则左子树上所有结点的值都小于它的根结点的值；
   • 若它的右子树不空，则右子树上所有结点的值都大于它的根结点的值；
   • 它的左、右子树也分别为二叉搜索树
2. 二叉搜索树的中序遍历结果是一个递增序列

根据性质 2，显然最小绝对差的出现范围，只会在中序遍历结果的相邻元素差之中，没有其他的选择。

那么本题的解题思路就很清晰了：使用中序遍历来遍历此二叉树，在这个过程中获取当前节点和前一个节点的差值，并迭代记录当前遍历进度中的差值最大值。

并且中序遍历二叉树有递归和迭代两种方法。

代码展示

中序遍历+递归法

TreeNode prev=null; // 记录中序遍历过程中的前一个节点

int ans=Integer.MAX_VALUE;// 记录最小绝对差，初始化为无穷大

public boolean getMinimumDifference(TreeNode root){
    // 递归进行中序遍历
    return inorder(root);
    return ans;
}

public boolean inorder(TreeNode node){
    if(node==null){
        return true;
    }

    // 首先递归遍历左子树
    inorder(node.left);

    // 检查当前差值是否小于前一个差值
    if(prev!=null){
        ans=Math.min(node.val-pre.val,ans);
    }
    prev=node; // 更新prev为当前节点

    // 然后递归遍历右子树
    inorder(node.right);
}

时间复杂度：O(n)，其中n是树中的节点数。算法需要访问树中的每个节点一次。

空间复杂度：O(h)，其中h是树的高度。递归调用栈的深度由树的高度决定。在最坏的情况下（树完全倾斜），空间复杂度可以达到O(n)。

中序遍历+迭代法

上诉中的递归函数我们也可以用迭代的方式来实现，两种方式是等价的，区别在于递归的时候隐式地维护了一个栈，而我们在迭代的时候需要显式地将这个栈模拟出来，其他都相同，具体的代码思路如下：

1. 初始化：创建一个栈来保存遍历过程中的节点，一个 prev 变量来记录上一次访问的节点，一个 ans 变量记录最小绝对差。
2. 迭代遍历：使用 current 指针指向当前节点，初始时指向根节点 root。然后进入一个循环，直到 current 为 null 且栈为空。
3. 向左遍历：在循环中，首先尽可能地向左遍历，并将沿途的节点压入栈中。这一步确保了能够按照中序遍历的顺序访问每个节点。
4. 处理节点：当不能再向左遍历时，从栈中弹出一个节点进行处理。这个节点是当前中序遍历序列中的下一个节点。此时比较差值大小。
5. 转向右子树：处理完当前节点后，转向右子树并继续迭代过程。
6. 完成遍历：当所有节点都被正确处理时，遍历结束。

通过这种方法，算法首先访问最左侧的节点（最深的左子树），然后回到其父节点（根节点），最后处理右子树。这正好符合中序遍历的顺序（左-根-右）。使用栈来存储未来将要访问的节点，从而实现了迭代遍历，而不是使用递归。

代码展示

public int getMinimumDifference(TreeNode root){
    TreeNode prev=null; // 用于记录中序遍历过程中的前一个节点
    int ans=Integer.MAX_VALUE; //记录最小绝对差
    Deque<TreeNode> stack=new LinkedList<>();
    TreeNode current=root;
    while(current!=null||!stack.isEmpty()){
        // 尽可能地向左遍历，并将沿途的节点压入栈
        while(current!=null){
        	stack.push(current);
        	current=current.left;
        }
        // 当到达最左侧节点后，弹出并处理节点
        current=stack.pop();
        if(prev!=null){
        	ans=Math.min(current.val-prev.val,ans);
        }
        prev=current;
        // 转向右子树
        current=current.right;
    }
    return ans;
}

时间复杂度：O(n)，其中 n 是二叉树的节点数。每一个节点恰好被遍历一次。

空间复杂度：O(h) ，其中h是树的高度。在最坏的情况下，栈中可能需要存储与树的高度相当数量的节点。对于一棵平衡二叉树，空间复杂度是O(log n) ，而对于非平衡二叉树，最坏情况下的空间复杂度可能达到O(n)。

总结

二叉搜索树的两大性质：

1. 二叉搜索树是一个有序树：
   • 若它的左子树不空，则左子树上所有结点的值都小于它的根结点的值；
   • 若它的右子树不空，则右子树上所有结点的值都大于它的根结点的值；
   • 它的左、右子树也分别为二叉搜索树
2. 二叉搜索树的中序遍历结果是一个递增序列