94.二叉树的中序遍历
难度:容易
给定一个二叉树的根节点 root ,返回 它的 中序 遍历 。
示例 1:
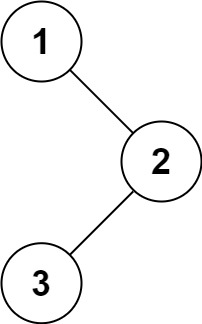
输入:root = [1,null,2,3]
输出:[1,3,2]示例 2:
输入:root = []
输出:[]示例 3:
输入:root = [1]
输出:[1]提示:
- 树中节点数目在范围
[0, 100]内 -100 <= Node.val <= 100
进阶: 递归算法很简单,你可以通过迭代算法完成吗?
递归算法
递归算法的三个要素:
- 确定递归函数的参数和返回值: 确定哪些参数是递归的过程中需要处理的,那么就在递归函数里加上这个参数, 并且还要明确每次递归的返回值是什么进而确定递归函数的返回类型。
- 确定终止条件: 写完了递归算法, 运行的时候,经常会遇到栈溢出的错误,就是没写终止条件或者终止条件写的不对,操作系统也是用一个栈的结构来保存每一层递归的信息,如果递归没有终止,操作系统的内存栈必然就会溢出。
- 确定单层递归的逻辑: 确定每一层递归需要处理的信息。在这里也就会重复调用自己来实现递归的过程。
每次写递归,都按照这三要素来写,可以保证写出正确的递归算法!
以前序遍历为例:
确定递归函数的参数和返回值:因为要打印出中序遍历节点的数值,所以参数里需要传入
result来放节点的数值,除了这一点就不需要再处理什么数据了也不需要有返回值,所以递归函数返回类型就是void,代码如下:javavoid inorder(TreeNode root, List<Integer> result)确定终止条件:在递归的过程中,如何算是递归结束了呢,当然是当前遍历的节点为空,那么本层递归就要结束了,所以如果当前遍历的这个节点是空,就直接
return,代码如下:javaif (root == null) { return; }确定单层递归的逻辑:中序遍历是左中右的循序,所以在单层递归的逻辑,要在中间取中节点的数值,代码如下:
javainorder(root.left, result); // 左 result.add(root.val); // 中 inorder(root.right, result); // 右
单层递归的逻辑就是按照左中右的顺序来处理的,这样二叉树的中序遍历,基本就写完了。
代码展示
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> result = new ArrayList<>();
inorder(root, result);
return result;
}
public void inorder(TreeNode root, List<Integer> result) {
if (root == null) {
return;
}
inorder(root.left, result);
result.add(root.val);
inorder(root.right, result);
}时间复杂度:O(n),其中 n 是二叉树的节点数。每一个节点恰好被遍历一次。
空间复杂度:O(n),为递归过程中栈的开销,平均情况下为 O(logn),最坏情况下树呈现链状,为 O(n)。
迭代法
上诉中的递归函数我们也可以用迭代的方式来实现,两种方式是等价的,区别在于递归的时候隐式地维护了一个栈,而我们在迭代的时候需要显式地将这个栈模拟出来,其他都相同,具体的代码思路如下:
- 创建辅助栈和结果列表: 使用一个栈
stack来存储未处理的节点,一个列表result用于存储遍历的结果。 - 遍历树: 使用一个
while循环来迭代遍历树。循环条件是当前节点不为null或栈不为空。- 处理左子树: 在每次循环中,首先尽可能地向左遍历。这是通过一个内层
while循环实现的,该循环将沿途的每个节点(包括根节点和根节点的左子节点)压入栈中。 - 访问节点: 当到达最左侧节点后(即当前节点为
null),从栈中弹出一个节点并将其值添加到结果列表中。这个节点就是中序遍历的下一个节点。 - 转向右子树: 最后,将当前节点转向刚处理过的节点的右子树,并重复上述过程。
- 处理左子树: 在每次循环中,首先尽可能地向左遍历。这是通过一个内层
外部的 while 循环条件 current != null || !stack.isEmpty() 是遍历过程的核心,它意味着遍历停止的条件是:
- 没有更多的节点可以向左遍历了(
current为null) - 栈中也没有其他待处理的节点(即所有节点都已访问完毕)
通过这种方法,算法首先访问最左侧的节点(最深的左子树),然后回到其父节点(根节点),最后处理右子树。这正好符合中序遍历的顺序(左-根-右)。使用栈来存储未来将要访问的节点,从而实现了迭代遍历,而不是使用递归。
代码展示
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> result = new ArrayList<>();
Deque<TreeNode> stack = new LinkedList<>();
TreeNode current = root;
while (current != null || !stack.isEmpty()) {
// 尽可能地向左遍历,并将沿途的节点压入栈
while (current != null) {
stack.push(current);
current = current.left;
}
// 当到达最左侧节点后,弹出并处理节点
current = stack.pop();
result.add(current.val);
// 转向右子树
current = current.right;
}
return result;
}时间复杂度:O(n),其中 n 是二叉树的节点数。每一个节点恰好被遍历一次。
空间复杂度:O(n),为迭代过程中显式栈的开销,平均情况下为 O(logn),最坏情况下树呈现链状,为 O(n)。
总结
迭代法比递归法更难想到。
